摘自:http://www.matrix67.com/blog/archives/6665#more-6665

在一根木棒上隨機選擇兩個點，並在這兩個點處下刀，把木棒砍成三段。下面哪種情況的可能性更大一些？

A．這三段木棒能拼成一個三角形
B．這三段木棒不能拼成一個三角形
C．上述兩種情況的出現概率相同

這個題目選B 。我們可以證明，這三段木棒能拼成三角形的概率是1/4 。不妨把這根木棒的長度設為1 ，兩個分割點的位置分別記作x 、 y ，則x 和y 都是0 到1 之間的隨機數。那麼，所有可能的(x, y) 組合就對應了正方形(0, 1) × (0, 1) 內的所有點。三段木棒能拼成三角形，當且僅當(x, y) 落在了陰影部分。由於陰影部分佔了總面積的1/4 ，因此這三段木棒能拼成三角形的概率就是1/4 。

這個題目還有很多變種。比如，如果先把木棒隨機砍成兩段，再把較長的那段木棒隨機砍成兩段，問這三段木棒能拼成一個三角形的概率是多少。這該怎麼解呢？你或許會說，為何不像剛才那樣，把第一個分割點和第二個分割點的位置分別記作x 、 y ，然後套用剛才的面積大法？這次就不行了，因為y 的值不再能獨立而均勻地分佈在0 到1 之間。但是，我們可以令x 為第一個分割點在整根木棒上的比例，令y 為第二個分割點在較長的那段木棒上的比例。舉個例子， (x, y) = (1/3, 1/3) 的意思就是，先把整根木棒砍成1 : 2 兩段，再把較長的那段木棒砍成1 : 2兩段。這樣一來，所有可能的(x, y) 組合就再一次均勻地對應了正方形(0, 1) × (0, 1) 內的所有點。最終，三段木棒能拼成三角形，當且僅當(x, y) 落在由x · y < 1/2, (1 – x) · y < 1/2, x · (1 – y) < 1/2, (1 – x) · (1 – y) < 1/2 組成的交集區域裡。利用定積分可以求出，這部分區域的面積佔整個正方形面積的2 · ln(2) – 1 ≈ 38.63% 。這就是答案。

著名的Buffon 投針問題，標準解法之一也用到了這種模型。在地板上畫一系列間隔為1 厘米的平行直線，然後把一根1 厘米長的針扔到地板上，它與直線有交點的概率是多少？令x 為這根針的中心到離它最近的那條直線的距離，令y 為這根針與平行線的夾角。所有可能的針的位置，就可以用所有可能的(x, y) 組合來表示，它們正好對應了矩形(0, 1/2) × (0, π/2) 內的所有點。其中，合法的區域為y < arccos(2x) ，它佔矩形面積的2 / π ≈ 63.66% 。這就是答案。

高中數學課本把這種解決概率問題的模型叫做“幾何概型”。說到幾何概型，最經典的可能要算下面這個例題。A 、 B 兩人約定好晚上6:00 到7:00 之間在公園門口見面。每個人都會從6:00 到7:00 這段時間當中隨機挑選一個時間，並在這個時間到達公園門口。每個人都只願意等待15 分鐘，也就是說，如果15 分鐘之後沒有看見對方，那麼就立即離開。那麼，兩人最終能見面的概率有多大？答案是7/16 。

答案是有的，而且這個簡單的方法甚至不需要語言。
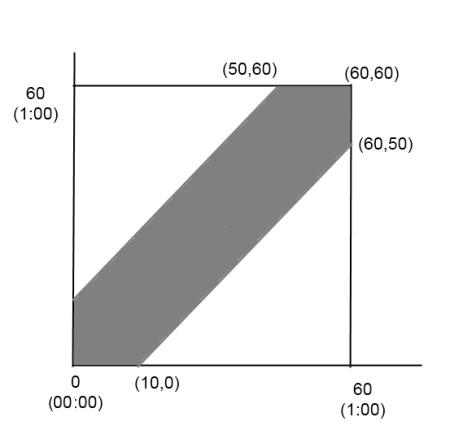從上圖中，你能一眼看出結果麼？
如果把甲的到達的時間記在x 軸上，把乙的到達時間記在y 軸上，那麼他們到達的時間便可以用坐標系中的點( x , y ) 來表示，根據設定可知這個點一定會落在圖中的正方形區域中。而如果二人想見面，那麼他們先後到達的時間間隔一定要小於十分鐘，即| x – y | ≤ 10。
解這個不等式，可得x – 10 ≤ y ≤ x + 10 。將這兩條支線在坐標系中畫出來，就能發現它們圍成的區域正好是上圖的陰影部分。
換言之，如果兩人要碰面，對應的到達的時間點（x，y） 就必須要落在陰影部分內。所以陰影部分的面積與大正方形面積之比就是所要求的概率，據此我們就能很輕鬆地計算出答案：11／36。