掛畫問題

2011年度最变态的迷宫难题

    下面大家将会看到的是一个极其简单而又极其复杂的“迷宫”，这无疑是我在本年度见到的最变态的谜题：从左边入口处的 2011 进去，在迷宫里转悠，最后变成 2012 从右边出来。你可以在迷宫里转圈，可以重复之前走过的路，但不能往回退着走。

      

    你能成功走出来吗？

    放弃吧，答案是

2011 +7 ÷2 +7 ÷2 +7 -5 ×3 ÷2 +7 ÷2 +7 ×3 -5 ÷2 +7 ÷2 +7 -5 ×3 -5 ×3 ÷2 +7 -5 ×3 ÷2 +7 -5 = 2012

    这个变态的谜题来自 Holiday Puzzles 2011 ，作者是 Erich Friedman 。
    提前祝大家新年快乐。

12個經典的行程問題

    無論是小學奧數，還是公務員考試，還是公司的筆試面試題，似乎都少不了行程問題——題目門檻低，人人都能看懂；但思路奇巧，的確會難住不少人。平時看書上網與人聊天和最近與小學奧數打交道的過程中，我收集到很多簡單有趣而又頗具啟發性的行程問題，在這裡整理成一篇文章，和大家一同分享。這些題目都已經非常經典了，絕大多數可能大家都見過；希望這裡能有至少一個你沒見過的題目，也歡迎大家來信提供更多類似的問題。

    讓我們先從一些最經典最經典的問題說起吧。選中空白部分顯示答案。

    甲、乙兩人分別從相距100 米的A 、B 兩地出發，相向而行，其中甲的速度是2 米每秒，乙的速度是3 米每秒。一隻狗從A 地出發，先以6 米每秒的速度奔向乙，碰到乙後再掉頭沖向甲，碰到甲之後再跑向乙，如此反复，直到甲、乙兩人相遇。問在此過程中狗一共跑了多少米？

    這可以說是最經典的行程問題了。不用分析小狗具體跑過哪些路程，只需要注意到甲、乙兩人從出發到相遇需要20秒，在這20秒的時間裡小狗一直在跑，因此它跑過的路程就是120米。
    說到這個經典問題，故事可就多了。下面引用某個經典的數學家八卦帖子： John von Neumann曾被問起一個中國小學生都很熟的問題：兩個人相向而行，中間一隻狗跑來跑去，問兩個人相遇後狗走了多少路。訣竅無非是先求出相遇的時間再乘以狗的速度。Neumann當然瞬間給出了答案。提問的人失望地說你以前一定聽說過這個訣竅吧。Neumann驚訝道：“什麼訣竅？我就是把狗每次跑的都算出來，然後計算無窮級數⋯⋯”

    某人上午八點從山腳出發，沿山路步行上山，晚上八點到達山頂。不過，他並不是勻速前進的，有時慢，有時快，有時甚至會停下來。第二天，他早晨八點從山頂出發，沿著原路下山，途中也是有時快有時慢，最終在晚上八點到達山腳。試著說明：此人一定在這兩天的某個相同的時刻經過了山路上的同一個點。

    這個題目也是經典中的經典了。把這個人兩天的行程重疊到一天去，換句話說想像有一個人從山腳走到了山頂，同一天還有另一個人從山頂走到了山腳。這兩個人一定會在途中的某個地點相遇。這就說明了，這個人在兩天的同一時刻都經過了這裡。

      

    甲從A 地前往B 地，乙從B 地前往A 地，兩人同時出發，各自勻速地前進，每個人到達目的地後都立即以原速度返回。兩人首次在距離A 地700 米處相遇，後來又在距離B 地400 米處相遇。求A 、 B 兩地間的距離。

    答案： 1700 米。第一次相遇時，甲、乙共同走完一個AB 的距離；第二次相遇時，甲、乙共同走完三個AB 的距離。可見，從第一次相遇到第二次相遇的過程花了兩個從出發到第一次相遇這麼多的時間。既然第一次相遇時甲走了700 米，說明後來甲又走了1400 米，因此甲一共走了2100 米。從中減去400 米，正好就是A 、 B 之間的距離了。

    甲、乙、丙三人百米賽跑，每次都是甲勝乙10 米，乙勝丙10 米。則甲勝丙多少米？

    答案是19 米。“乙勝丙10 米”的意思就是，等乙到了終點處時，丙只到了90 米處。“甲勝乙10 米”的意思就是，甲到了終點處時，乙只到了90 米處，而此時丙應該還在81 米處。所以甲勝了丙19 米。

    哥哥弟弟百米賽跑，哥哥贏了弟弟1 米。第二次，哥哥在起跑線處退後1 米與弟弟比賽，那麼誰會獲勝？

    答案是，哥哥還是獲勝了。哥哥跑100 米需要的時間等於弟弟跑99 米需要的時間。第二次，哥哥在-1 米處起跑，弟弟在0 米處起跑，兩人將在第99 米處追平。在剩下的1 米里，哥哥超過了弟弟並獲得勝利。

    如果你上山的速度是2 米每秒，下山的速度是6 米每秒（假設上山和下山走的是同一條山路）。那麼，你全程的平均速度是多少？

    這是小學行程問題中最容易錯的題之一，是小孩子們死活也搞不明白的問題。答案不是4米每秒，而是3米每秒。不妨假設全程是S米，那麼上山的時間就是S/2 ，下山的時間就是S/6 ，往返的總路程為2S ，往返的總時間為S/2 + S/6 ，因而全程的平均速度為2S / (S/2 + S/6) = 3 。
    其實，我們很容易看出，如果前一半路程的速度為a ，後一半路程的速度為b ，那麼總的平均速度應該小於(a + b) / 2 。這是因為，你會把更多的時間花在速度慢的那一半路程上，從而把平均速度拖慢了。事實上，總的平均速度應該是a和b的調和平均數，即2 / (1/a + 1/b) ，很容易證明調和平均數總是小於等於算術平均數的。

    接下來的兩個問題與流水行船有關。假設順水時實際船速等於靜水中的船速加上水流速度，逆水時實際船速等於靜水中的船速減去水流速度。

    船在靜水中往返A 、 B 兩地和在流水中往返A 、 B 兩地相比，哪種情況下更快？

    這是一個經典問題了。答案是，船在靜水中更快一些。注意船在順水中的實際速度與在逆水中的實際速度的平均值就是它的靜水速度，但由前一個問題的結論，實際的總平均速度會小於這個平均值。因此，船在流水中往返需要的總時間更久。
    考慮一種極端情況可以讓問題的答案變得異常顯然，頗有一種荒謬的喜劇效果。假設船剛開始在上游。如果水速等於船速的話，它將以原速度的兩倍飛速到達折返點。但它永遠也回不來了⋯⋯

    船在流水中逆水前進，途中一個救生圈不小心掉入水中，一小時後船員才發現並調頭追趕。則追上救生圈所需的時間會大於一個小時，還是小於一個小時，還是等於一個小時？

    這也是一個經典問題了。中學物理競賽中曾出現過此題，《編程之美》上也有一個完全相同的問題。答案是等於一個小時。原因很簡單：反正船和救生圈都被加上了一個水流的速度，我們就可以直接拋開流水的影響不看了。換句話說，我們若以流水為參照系，一切就都如同沒有流水了。我們直接可以想像船在靜水噹中丟掉了一個救生圈並繼續前行一個小時，回去撿救生圈當然也還需要一個小時。
    每當有人還是沒想通時，我很願意舉這麼一個例子。假如有一列勻速疾馳的火車，你在火車車廂裡，從車頭往車尾方向步行。途中你掉了一個錢包，但繼續往前走了一分鐘後才發現。顯然，你回去撿錢包需要的時間也是一分鐘。但是，錢包不是正被火車載著自動地往遠方走嗎？其實，既然你們都在火車上，自然就可以無視火車的速度了。前面的救生圈問題也是一樣的道理。

    下面這個問題也很類似：假設人在傳送帶上的實際行走速度等於人在平地上的行走速度加上一個傳送帶的速度。

    你需要從機場的一號航站樓走到二號航站樓。路途分為兩段，一段是平地，一段是自動傳送帶。假設你的步行速度是一定的，因而在傳送帶上步行的實際速度就是你在平地上的速度加上傳送帶的速度。如果在整個過程中，你必須花兩秒鐘的時間停下來做一件事情（比如蹲下來系鞋帶），那麼為了更快到達目的地，你應該把這兩秒鐘的時間花在哪裡更好？

    這個漂亮的問題出自Terence Tao 的Blog （http://terrytao.wordpress.com/2008/12/09/an-airport-inspired-puzzle）。很多人可能會認為，兩種方案是一樣的吧？然而，真正的答案卻是，把這兩秒花在傳送帶上會更快一些。這是因為，傳送帶能給你提供一些額外的速度，因而你會希望在傳送帶上停留更久的時間，更充分地利用傳送帶的好處。因此，如果你必須停下來一會兒的話，你應該在傳送帶上多停一會兒。

    假設你站在甲、乙兩地之間的某個位置，想乘坐出租車到乙地去。你看見一輛空車遠遠地從甲地駛來，而此時整條路上並沒有別人與你爭搶空車。我們假定車的行駛速度和人的步行速度都是固定不變的，並且車速大於人速。為了更快地到達目的地，你應該迎著車走過去，還是順著車的方嚮往前走一點？

    这是我在打车时想到的一个问题。我喜欢在各种人多的场合下提出这个问题，此时大家的观点往往会立即分为鲜明的两派，并且各有各的道理。有人说，由于车速大于人速，我应该尽可能早地上车，充分利用汽车的速度优势，因此应该迎着空车走上去，提前与车相遇嘛。另一派人则说，为了尽早到达目的地，我应该充分利用时间，马不停蹄地赶往目的地。因此，我应该自己先朝目的地走一段路，再让出租车载我走完剩下的路程。
    其实答案出人意料的简单，两种方案花费的时间显然是一样的。只要站在出租车的角度上想一想，问题就变得很显然了：不管人在哪儿上车，出租车反正都要驶完甲地到乙地的全部路程，因此你到达乙地的时间总等于出租车驶完全程的时间，加上途中接人上车可能耽误的时间。从省事儿的角度来讲，站在原地不动是最好的方案！
    我曾经把这个有趣的问题搬上了《新知客》杂志 2010 年第 9 期的趣题专栏（http://www.matrix67.com/blog/archives/3677）。不少人都找到了这个题的一个 bug ：在某些极端情况下，顺着车的方向往前走可能会更好一些，因为你或许会直接走到终点，而此时出租车根本还没追上你！

    某工厂每天早晨都派小车按时接总工程师上班。有一天，总工程师为了早些到工厂，比平日提前一小时出发步行去工厂。走了一段时间后，遇到来接他的小车才上车继续前进。进入工厂大门后，他发现只比平时早到 10 分钟。总工程师在路上步行了多长时间才遇到来接他的汽车？设人和汽车都做匀速直线运动。

    据说，这是一道初中物理竞赛题（初中物理有“运动”一章）。答案是 55 分钟。首先，让我们站在车的角度去想（正如前一题那样）。车从工厂出发，到半途中就遇上了总工程师并掉头往回走，结果只比原来早到 10 分钟。这说明，它比原来少走了 10 分钟的车程，这也就是从相遇点到总工程师家再到相遇点的路程。这就说明，从相遇点到总工程师家需要 5 分钟车程。
    现在，让我们把视角重新放回总工程师那里。让我们假设总工程师遇上了来接他的车并坐上去之后，并没有下令汽车立即掉头，而是让车像平日那样继续开到他家再返回工厂，那么他到工厂的时间应该和原来一样。这说明，他提前出发的那一个小时完全浪费了。这一个小时浪费在哪儿了呢？浪费在了他步行到相遇点的过程，以及乘车又回到家的过程。既然乘车又回到家需要 5 分钟，因此步行的时间就是 55 分钟了。

    有一位隐居在深山老林的哲学家。一天，他忘记给家里唯一的时钟上发条了。由于他家里没有电话、电视、网络、收音机等任何能获知时间的设备，因此他彻底不知道现在的时间是多少了。于是，他徒步来到了他朋友家里坐了一会儿，然后又徒步回到自己家中。此时，他便知道了应该怎样重新设定自己的时钟。他是怎么做的？
    很多人的第一想法或许是观察日出日落。在此，我们也假设通过太阳位置判断时间是不可靠的。 Update: 不少网友找到了此题的一个 bug 。在此我们假设，时钟是固定在墙上的，或者由于太重，无法直接带走。

    传统意义上说，这个问题不算行程问题。不过，在写这篇文章时，这个问题立即跳入我的脑海，我也就把它放进来了。
    答案：别忘了，他家里的时钟并不是不走了，只是不准了而已。因此，他可以借助自己家里的时钟，判断他此次出行一共花了多久。假设往返所花时间一样，再结合在朋友那儿看到的正确时间，他便能算出应该怎样调整自己的时钟了。

还有几个不太相关的经典问题这里没有提到，不过你或许会感兴趣：
汽车穿越沙漠问题：http://en.wikipedia.org/wiki/Jeep_problem
木杆上的蚂蚁：http://www.matrix67.com/blog/archives/3791 计算题1

贴着另一枚硬币旋转一周则自身转了两周：不同的解释方法

    有一道非常经典的智力问题：假设有两个一模一样的硬币 A 和硬币 B ，如果让硬币 B 不动，让硬币 A 贴着硬币 B 旋转一周，那么硬币 A 自身旋转了多少周？一个常见的错误答案是“显然也是一周啊”，而实际上正确的答案是两周，如下图所示。我们有很多方法来解释这种现象，其中最传统的说法便是“公转了一周，自转了一周”。硬币 A 的运动是由两部分合成的，公转一周（想像一个人绕着地球走了一圈），以及自转一周（想像一个轮子在地面上滚动了一周）。想像你是站在硬币 B 中心处的一个小人儿，看着硬币 A 贴着你脚下的硬币转动一圈。如果在此过程中，你始终面向硬币 A ，那么在你看来，硬币 A 似乎就是在长为 2πr 的平地上滚了一圈。而实际上，在观察硬币 A 的过程中，你自己也原地转了 360 度，因此从外面的人看来，硬币实际上转了两周。

      

    写了这篇文章后，我习惯性地开始用正多边形逼近的思路去分析一些与圆有关的一般性结论。在准备一份初中几何问题的材料时，我突然想到了上述问题的一个简单而漂亮的解释方法。

      

    考虑一个正方形贴着另一个正方形旋转一周，你会发现，前者自身也旋转了两周。容易验证，对于正三角形和正六边形，情况也都是如此。这一定不是巧合，或许对于所有的正 n 边形，结论都同样成立。仔细一想，你发现这很容易理解：对于正 n 边形来说，每转过一个顶点，转过的角度都相当于正 n 边形两个外角的大小。转过 n 个顶点回到出发位置后，正 n 边形显然转过了两倍的外角和，也就是 720 度。因而，正 n 边形自身旋转了两周。当正多边形的边数趋于无穷多时可知，一枚硬币贴着另一枚硬币旋转一周，则这枚硬币自身也一定正好旋转了两周。

不用三角函数求出∠BAC的度数

http://www.matrix67.com/blog/archives/5398#more-5398

趣题：不用三角函数求出∠BAC的度数

    今天看到了一道很有趣的几何题。如图，四边形 ABCD 中，连接对角线 AC 、 BD ，若 ∠ABD = 40° ， ∠ADB = 80° ， ∠CBD = 70° ， ∠CDB = 50° ，求 ∠BAC 的度数。

      

    这道题看上去似乎非常简单，但稍作尝试你就会发现，仅仅是在这几个角度之间来回倒腾，是没法求出 ∠BAC 的度数的。听说过 Langley 问题（就是那个臭名昭著的 20-80-80 三角形）的人就会知道，这种类型的题目往往会非常非常地复杂。据说这是 1989 – 1990 年加拿大亚伯达省中学数学竞赛中的一道题目，当时只有一个人做对，并且解答过程用到了非常繁琐的三角函数运算。然而，这道题实际上有一个非常漂亮的秒杀方法，完全不需要使用三角函数。你能想到吗？

      

    答案：把注意力集中在三角形 ABD 上。容易看出， ∠A = 180° – 40° – 80° = 60° 。另外， CB 平分 ∠B 的外角， CD 平分 ∠D 的外角，因而 C 就是三角形 ABD 的一个旁心。这说明， CA 也将平分 ∠A 。因此， ∠BAC = 60° / 2 = 30° 。

参考资料： Andy Liu, “A Better Angle From Outside”, Mathematical Horizons, November 1997

Marden定理

http://www.matrix67.com/blog/archives/5480#more-5480

數學之美：Marden定理

    如果叫我說出一個我最喜歡的數學定理，之前我可能會說Monge 定理；不過現在，我可能會說Marden 定理了：

         

設p(z)是一個複數域上的三次多項式， z 1、 z 2、 z 3是p(z)的三個根，它們在復平面上不共線。那麼，在這個複平面上存在唯一的橢圓，使得它與三角形z 1 z 2 z 3的各邊都相切，並且都切於各邊的中點處。並且，這個橢圓的兩個焦點是p'(z)的兩根。

    讀完這個結論以後，你一定會被數學之美深深地打動。這個結論出現在了Morris Marden於1945年發表的一篇論文裡，因而被Dan Kalman稱為Marden定理。Marden本人則認為，這個結論最早是由Jörg Siebeck在1864年發現並證明的。下面我們簡單地來證明一下這個結論，證明過程出自Dan Kalman在2008年發表的獲獎論文An Elementary Proof of Marden's Theorem。

    其實，結論的前半部分並不奇怪，對於任意一個三角形，內切於各邊中點的橢圓本來就是唯一的。這是很容易證明的，其中一種證明方法是，通過線性變換把這個三角形變形成一個等邊三角形，那麼內切於各邊中點的橢圓現在仍然是內切於各邊中點的橢圓，然而在一個等邊三角形中，內切於各邊中點的橢圓只有一個，就是這個等邊三角形的內切圓。關於這一點，詳細的證明可以參見這裡。

    因此， Marden 定理的核心就是：為什麼這個橢圓的兩個焦點就是p'(z) 的兩根。

    首先，讓我們來說明，為了證明Marden定理，我們可以把三角形z 1 z 2 z 3放置在復平面上的任意一個對我們有利的位置。因為，如果對於復平面上的某一個三角形來說命題是成立的，那麼任意地對這個三角形進行縮放、旋轉、平移，命題仍然是成立的。為什麼？這是因為，對三角形的縮放、旋轉、平移，說白了就是對三角形中的各個點進行變換操作M(z) = αz + β ，其中α和β是兩個固定的複數常數，並且α ≠ 0 。讓z與α相乘的結果就是對z進行縮放和旋轉，而β則表示在此之後平移量的大小。假設我們的命題對三角形z 1 z 2 z 3成立，對整個複平面進行上述變換後，三角形的三個頂點就分別移到了M(z 1 ) 、 M(z 2 ) 、 M(z 3 ) 。同時，三角形的內切橢圓以及橢圓的兩個焦點也都被順帶著移動了過去，內切橢圓還是內切橢圓，橢圓的焦點也還是橢圓的焦點。另外，原來的多項式是p(x) = (z – z 1 )(z – z 2 )(z – z 3 ) ，變換之後，新的多項式p M (x)就變成了(z – M( z 1 ))(z – M(z2 ))(z – M(z 3 )) 。假設原橢圓的兩個焦點分別是f 1和f 2，我們已經知道了它們正好是p'(z)的兩根。我們想要確認的就是，新橢圓的兩個焦點M(f 1)和M(f 2 )正好就是p M '(z)的兩個根。

    把p M (z)中的z全部用M(z)代換，得到：

         p M (M(z)) = (M(z) – M(z 1 ))(M(z) – M(z 2 ))(M(z) – M(z 3 ))

    注意到M(z) – M(z 1 )就等於α(z – z 1 ) （因為β被抵消了），同理，上式的後面兩個因式也分別等於α(z – z 2 )和α(z – z 3 ) 。於是，整個上式化簡為：

         p M (M(z)) = α 3 (z – z 1 )(z – z 2 )(z – z 3 )

    即：

         p M (M(z)) = α 3 · p(z)

    現在，在等式兩邊同時取導數（注意到M'(z) = α ），於是得到：

         α · p M '(M(z)) = α 3 · p'(z)

    也就是：

         p M '(M(z)) = α 2 · p'(z)

    這說明，如果f 1是p'(z)的根，那麼M(f 1 )也將是p M '(z)的根；類似地，如果f 2是p'(z)的根，那麼M (f 2 )也將是p M '(z)的根。這正是我們剛才想要說明的事情。

         

    為了證明Marden定理，我們還有一個準備工作要做。讓我們來證明下面這個引理：如圖， F 1、 F 2是給定橢圓的兩個焦點，過橢圓外的一點A向橢圓作兩條切線，切點分別為G 1和G 2，則有∠F 1 AG 1 = ∠F 2 AG 2。其實，這個引理包含了兩種不同的情況，如果把上面的G 1和G 2兩個點反過來標，我們將會得到另外一種情況。不過，如果我們證明了在第一種情況下結論始終成立，第二種情況也就自動地獲證了。因此，我們可以直接假設G 1和G 2的標法就如上圖所示。

         

    證明這個引理需要用到與橢圓有關的一個非常經典的結論：從其中一個焦點出發的光線，射向橢圓內壁的任意一個位置，反射光線總會經過這個橢圓的另外一個焦點。換句話說，在上圖當中，過橢圓上的點T作切線，則∠1將會等於∠2 。你可以在這裡看到與橢圓的這個性質有關的更多討論。

         

    現在，沿著切線AG 1將F 1翻折到H 1，那麼H 1、 G 1、 F 2將會共線。類似地，沿著切線AG 2將F 2翻折到H 2，那麼H 2、 G 2、 F 1也將會共線。為了證明∠F 1 AG 1 = ∠F 2 AG 2，我們只需要證明∠F 1 AH 1 = ∠F 2 AH 2即可。

    由於H 1 F 2 = H 1 G 1 + G 1 F 2 = F 1 G 1 + G 1 F 2 = F 1 G 2 + G 2 F 2 = F 1 G 2 + G 2 H 2 = F 1 H 2，另外由剛才的翻折可知F 1 A = H 1 A ，並且F 2 A = H 2 A ，於是三角形AH 1 F 2和三角形AF 1 H2全等。這告訴我們∠H 1 AF 2 = ∠F 1 AH 2，同時減去一個公共部分後即得∠F 1 AH 1 = ∠F 2 AH 2，引理也就證到了。

    現在，我們已經準備好證明Marden定理了。我們首先說明，以p'(z)的兩根為焦點的橢圓，如果經過三角形z 1 z 2 z 3某條邊上的中點，則它一定會與這條邊相切。為此，我們把三角形的三個頂點擺放到復平面上的-1 、 1和w = a + bi三個位置，其中b > 0 ，於是p(z) = (z – 1)(z + 1)(z – w) = z 3 – w · z 2 – z + w 。對p(z)求導後得p'(z) = 3 · z 2 – 2 · w · z – 1 。

         

    假設p'(z)的兩根是f 1和f 2，則兩根之和f 1 + f 2 = 2 · w / 3 ，兩根之積f 1 · f 2 = – 1 / 3 。前一個式子說明了f 1和f 2當中至少有一個在x軸上方，而在後一個式子中， f 1 · f 2居然沒有虛數部分，這就說明了f 1和f 2其實都在x軸上方，並且θ 1 + θ 2 = 180° 。因而，如果以f 1和f 2為焦點，作一個過原點0的橢圓，則x軸就是一條經過該點的直線，它滿足∠1 = ∠2 ，這表明x軸就是橢圓在該點處的切線。而x軸其實就是三角形的底邊，原點0正是三角形底邊的中點！

    由於以同一對點為焦點只能作出一個與給定直線相切的橢圓，因而這就順便說明了，以p'(z)的兩根為焦點的橢圓，如果與三角形z 1 z 2 z 3的某條邊相切，則它一定會與這條邊切於中點處。

    最後我們來說明，以p'(z)的兩根為焦點的橢圓，如果與三角形z 1 z 2 z 3的其中一條邊相切了，則它一定會與三角形的三條邊都相切。由剛才的推論可知，所有的切點都將會是中點， Marden定理就證到了。這一次，讓我們把三角形的三個頂點放在0 、 1 、 w = a + bi三個位置，其中b > 0 。稍後我們將會看到，以p'(z)的兩根為焦點並且切於底邊的橢圓也會與0w相切。由對稱性，它一定也會和第三條邊相切。

    取p(z) = z(z – 1)(z – w) = z 3 – (1 + w) · z 2 + w · z 。求導得： p'(z) = 3 · z 2 – 2 · (1 + w) · z + w 。

         

    假設p'(z)的兩根是f 1和f 2。剛才我們已經知道了， f 1和f 2一定都在x軸的上方。不過這一次，兩根之積f 1 · f 2等於w / 3 。這告訴了我們什麼？這告訴了我們， θ 1 + θ 2 = θ ，換句話說， ∠1 = ∠2 ！假設以f 1和f 2為焦點作了一個橢圓， x軸正好是一條切線，那麼根據前面我們證過的那個結論，經過原點的另一條切線將會滿足∠1 = ∠2 ，這說明它與0w這條線重合。因而， 0w就是這另外一條切線。這就完成了Marden定理的最後一環。

26 個比較概率大小的問題

你的數學直覺怎麼樣？你能憑藉直覺，迅速地判斷出誰的概率大，誰的概率小嗎？下面就是26 個這樣的問題。如果你感興趣的話，你可以先掃一遍所有的問題，再逐一閱讀答案，看看你猜對了多少。這篇文章很長，你可以考慮把它加入書籤，每天看幾個問題。

1．A 、 B 、 C 、 D 四人玩撲克牌遊戲， A 、 C 兩人同盟， B 、 D 兩人同盟。將除去大小王的52 張牌隨機分發給四人（每人獲得13 張牌）後，下面哪種情況的可能性更大一些？

A．A 、 C兩人手中都沒有梅花
B．A 、 C兩人手中囊括了所有的梅花
C．上述兩種情況的出現概率相同

A 、 C 兩人手中都沒有梅花，等價於B 、 D 兩人手中囊括了所有的梅花，它的概率與A 、 C 兩人手中囊括所有梅花的概率相同。因此，這個問題的答案顯然是C 。

2．我給10 個好朋友分別寫了一封信，並把這10 個人的地址分別寫在了10 個信封上。如果我隨機地將這10 封信裝進10 個信封裡（每封信都裝進了一個不同的信封裡），下面哪種情況的可能性更大一些？

A．恰好有9封信裝進了正確的信封
B．所有10封信都裝進了正確的信封
C．上述兩種情況的出現概率相同

你或許會以為，全都裝對的可能性很低，裝錯一個的可能性則略高一些。然而事實上，這道題的答案是B 。原因非常簡單：恰好有9 封信裝對，這是根本不可能的——如果其中9 封信都裝對了，剩下的那一封信肯定也裝對了。

實際上， 10 封信的排列方式一共有10! = 3628800 種，其中裝對的信有0, 1, 2, 3, …, 9, 10 封的情況數分別為1334961, 1334960, 667485, 222480, 55650, 11088, 1890, 240, 45, 0, 1 。可以看到，絕大多數時候，這個數列裡的數都是不斷遞減的；也就是說，裝對的信越多，概率就越低，這個直覺確實是準確的。唯一的例外，就是這個數列的最後兩項，其背後的原因正如剛才所說。

你或許發現了一個有趣的現象：數列的第二項正好比第一項小1 。這並不是巧合。有一個普遍的規律是，假設把n 封信裝進n 個信封裡，那麼當n 為偶數時，裝對1 封信的情況數比全都裝錯的情況數少1 ，當n 為奇數時，裝對1 封信的情況數比全都裝錯的情況數多1 。我們下面就來證明這一點。

假設把n封信裝進n個信封裡，全都裝錯的情況有D n種。那麼，數列D 1 , D 2 , D 3 , …滿足一個非常簡單的遞推關係： D n = (n – 1) (D n-1 + D n-2 ) 。為什麼呢？我們慢慢來分析。由於每封信都裝錯了，因此第1封信沒有裝進1號信封。無妨假設它裝進了2號信封。那麼，第2封信裝到哪兒去了呢？如果第2封信正好裝進了1號信封，那麼剩下的n – 2封信就有D n-2種可能的裝法。如果第2封信沒有裝進1號信封呢？情況就變成了這樣：第2, 3, 4, …, n封信裝進了編號分別為1, 3, 4, …, n的信封裡，其中第2封信不在1號信封裡，第3封信不在3號信封裡，第4封信不在4號信封裡……總之，這n – 1封信中，每封信都正好有一個禁放的信封。於是，這就構成了D n-1種可能的裝法。當然，第1封信也有可能裝進了3號信封裡，也有可能裝進了4號信封裡……因此，我們就有D n = (n – 1) (D n-1 + D n-2 ) 。

在這個式子的左右兩邊同時減去n · D n-1，於是得到：

D n – n · D n-1 = – (D n-1 – (n – 1) · D n-2 )

令A n = D n – n · D n-1，於是A n滿足遞推關係式：

A n = – A n-1

可以驗證：

A 2 = D 2 – 2 · D 1 = 1 – 0 = 1

於是有：

A n = (-1) n

即D n – n · D n-1 = (-1) n。而n · D n-1正好表示把n封信裝進n個信封裡恰好裝對1封信的情況數。

3．桌子上有A 、 B 兩個不透明的盒子，盒子A 裡有m 個白色小球和1 個黑色小球，盒子B 裡有n 個白色小球和1 個黑色小球。你需要先從盒子A 裡隨機取出一個小球，再從盒子B 裡隨機取出一個小球。如果兩個小球都是黑色的，那麼你就獲勝了。下面哪種情況下，你獲勝的概率更大一些？

A．m = 5，n = 5 
B．m = 4，n = 6 
C．上述兩種情況的獲勝概率相同

你或許會以為，反正都是10 個白色小球，怎麼放應該沒關係吧。而事實上，在A 、 B 兩種情況下，獲勝的概率還真的不一樣。在情況A 中，你獲勝的概率為(1/6) × (1/6) = 1/36 ；在情況B 中，你獲勝的概率為(1/5) × (1/7) = 1/ 35 。因此，這個題目的答案是B 。

如果我們把規則改為，先隨機選擇其中一個盒子，再從這個盒子中隨機取出一個小球，取到黑色小球即獲勝，那麼情況B 的獲勝概率仍然會更大一些。在情況A 中，你獲勝的概率為(1/2) × (1/6) + (1/2) × (1/6) = 1/6 ；在情況B 中，你獲勝的概率為(1 /2) × (1/5) + (1/2) × (1/7) = 6/35 。

如果你可以自己安排每個小球的位置（但黑白小球的總數不變），那麼不管是在原遊戲中還是在改版後的遊戲中，為了讓自己的勝率達到最大，你都應該在其中一個盒子裡只放1 個黑球，在另一個盒子裡放入剩下的1 個黑球和10 個白球。這樣的話，在原遊戲中，你獲勝的概率將達到1 × (1/11) = 1/11 ；在改版後的遊戲中，你獲勝的概率將達到(1/2) × 1 + (1/2 ) × (1/11) = 6/11 。

4．不透明的盒子裡有10 個白球和1 個黑球，你的目標是從中取出黑球。每次，你可以從中隨機取出一個小球，並觀察它的顏色：如果是黑球，則達到目標，結束操作；如果是白球，則將小球放回盒子裡，然後繼續像這樣隨機取球，直到取出了黑球為止。下面哪種情況的可能性更大一些？

A．第1次就取到了黑球
B．到第4次才取到黑球
C．上述兩種情況的出現概率相同

這個題目的答案顯然應該是A 。若每次取出黑球的概率為p ，則第1次就取到黑球的概率為p ，到第4次才取到黑球的概率為(1 – p) · (1 – p) · ( 1 – p) · p ，後者永遠比前者更低。如果我們把第n次才取到黑球的概率記為P n，那麼就有：

P n = (1 – p) n-1 · p

然而，把P 1 , P 2 , P 3 , …全部累加起來的結果應該為1 ，於是我們用概率論的方法得到公式：

(1 + (1 – p) + (1 – p) 2 + (1 – p) 3 + …) · p = 1

即：

1 + (1 – p) + (1 – p) 2 + (1 – p) 3 + … = 1 / p

令x = 1 – p ，得到：

1 + x + x 2 + x 3 + … = 1 / (1 – x)

這正是無窮等比級數的求和公式。由於實數p 必須在0 到1 之間，而x = 1 – p ，因此上式中的x 也必須在0 到1 之間。

5．不透明的盒子裡有10 個白球和1 個黑球。A 、 B 兩人輪流從盒子裡取球，每個人每次只能隨機從中取出一個小球（取出的小球不再放回）。誰先取到那個黑球，誰就獲得遊戲的勝利。如果A 先取，那麼理論上，下面哪種情況的可能性更大一些？

A．A獲得遊戲的勝利
B．B獲得遊戲的勝利
C．上述兩種情況的出現概率相同

這個題目的答案是A 。不妨規定，即使有人取到了黑球，兩人也繼續往下取，直到把所有的小球都取光。整個遊戲就可以等價地看作是，兩人輪流取完所有的小球後，看看誰手中有那個黑球。由於A 先取，因此最後A 會取到6 個小球， B 只能取到5 個小球。所以，黑球在A 手中的概率更大，等於6/11 。

類似地，如果不透明的盒子裡有W 個白球和B 個黑球，不斷從裡面取出小球（不再放回），那麼不管i 是多少（0 ​​< i ≤ W + B），第i 次取到的是白球的概率都是W / (W + B) ，第i 次取到的是黑球的概率都是B / (W + B) 。因為，這本質上相當於把所有的小球隨機地排成一排，問第i 個小球是白色或者黑色的概率。

6．不透明的盒子裡有2 個白球和5 個黑球。地上還有足夠多的白球和黑球。每次從盒子裡隨機取出兩個小球，放在地上。如果剛才取出的兩個小球都是白球，則從地上拿一個白球放入盒子；如果剛才取出的兩個小球都是黑球，則從地上拿一個白球放入盒子；如果剛才取出的兩個小球是一黑一白，則從地上拿一個黑球放入盒子。不斷重複，直至盒子裡只剩一個小球為止。那麼，下面哪種情況的可能性更大一些？

A．剩下的那個小球是白球

B．剩下的那個小球是黑球
C．上述兩種情況的出現概率相同

這是一個很賴皮的題目。它的答案是B 。事實上，出現情況A 的概率為0 ，出現情況B 的概率為100% 。原因很簡單。每次操作後，黑球的數量要么不變，要么減2 ，所以黑球的奇偶性始終保持相同。初始時盒子裡有奇數個黑球，今後盒子裡就永遠有奇數個黑球。所以，如果最後盒子裡剩了1 個小球，那它必然是黑球。

7．在一根木棒上隨機選擇兩個點，並在這兩個點處下刀，把木棒砍成三段。下面哪種情況的可能性更大一些？

A．這三段木棒能拼成一個三角形
B．這三段木棒不能拼成一個三角形
C．上述兩種情況的出現概率相同

這個題目選B 。我們可以證明，這三段木棒能拼成三角形的概率是1/4 。不妨把這根木棒的長度設為1 ，兩個分割點的位置分別記作x 、 y ，則x 和y 都是0 到1 之間的隨機數。那麼，所有可能的(x, y) 組合就對應了正方形(0, 1) × (0, 1) 內的所有點。三段木棒能拼成三角形，當且僅當(x, y) 落在了陰影部分。由於陰影部分佔了總面積的1/4 ，因此這三段木棒能拼成三角形的概率就是1/4 。

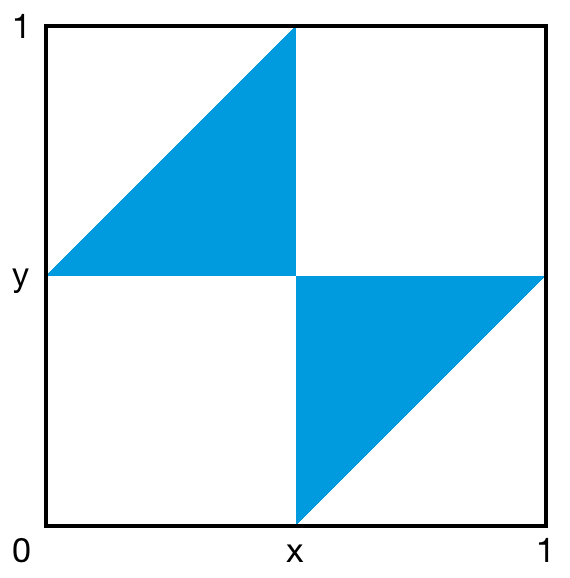
這個題目還有很多變種。比如，如果先把木棒隨機砍成兩段，再把較長的那段木棒隨機砍成兩段，問這三段木棒能拼成一個三角形的概率是多少。這該怎麼解呢？你或許會說，為何不像剛才那樣，把第一個分割點和第二個分割點的位置分別記作x 、 y ，然後套用剛才的面積大法？這次就不行了，因為y 的值不再能獨立而均勻地分佈在0 到1 之間。但是，我們可以令x 為第一個分割點在整根木棒上的比例，令y 為第二個分割點在較長的那段木棒上的比例。舉個例子， (x, y) = (1/3, 1/3) 的意思就是，先把整根木棒砍成1 : 2 兩段，再把較長的那段木棒砍成1 : 2兩段。這樣一來，所有可能的(x, y) 組合就再一次均勻地對應了正方形(0, 1) × (0, 1) 內的所有點。最終，三段木棒能拼成三角形，當且僅當(x, y) 落在由x · y < 1/2, (1 – x) · y < 1/2, x · (1 – y) < 1/2, (1 – x) · (1 – y) < 1/2 組成的交集區域裡。利用定積分可以求出，這部分區域的面積佔整個正方形面積的2 · ln(2) – 1 ≈ 38.63% 。這就是答案。

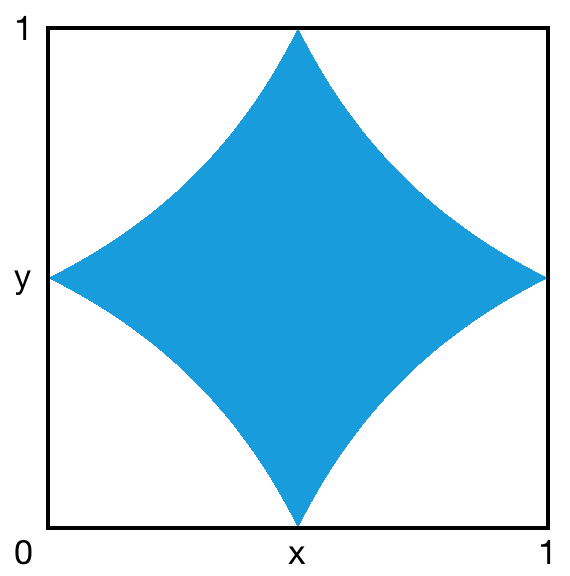
著名的Buffon 投針問題，標準解法之一也用到了這種模型。在地板上畫一系列間隔為1 厘米的平行直線，然後把一根1 厘米長的針扔到地板上，它與直線有交點的概率是多少？令x 為這根針的中心到離它最近的那條直線的距離，令y 為這根針與平行線的夾角。所有可能的針的位置，就可以用所有可能的(x, y) 組合來表示，它們正好對應了矩形(0, 1/2) × (0, π/2) 內的所有點。其中，合法的區域為y < arccos(2x) ，它佔矩形面積的2 / π ≈ 63.66% 。這就是答案。

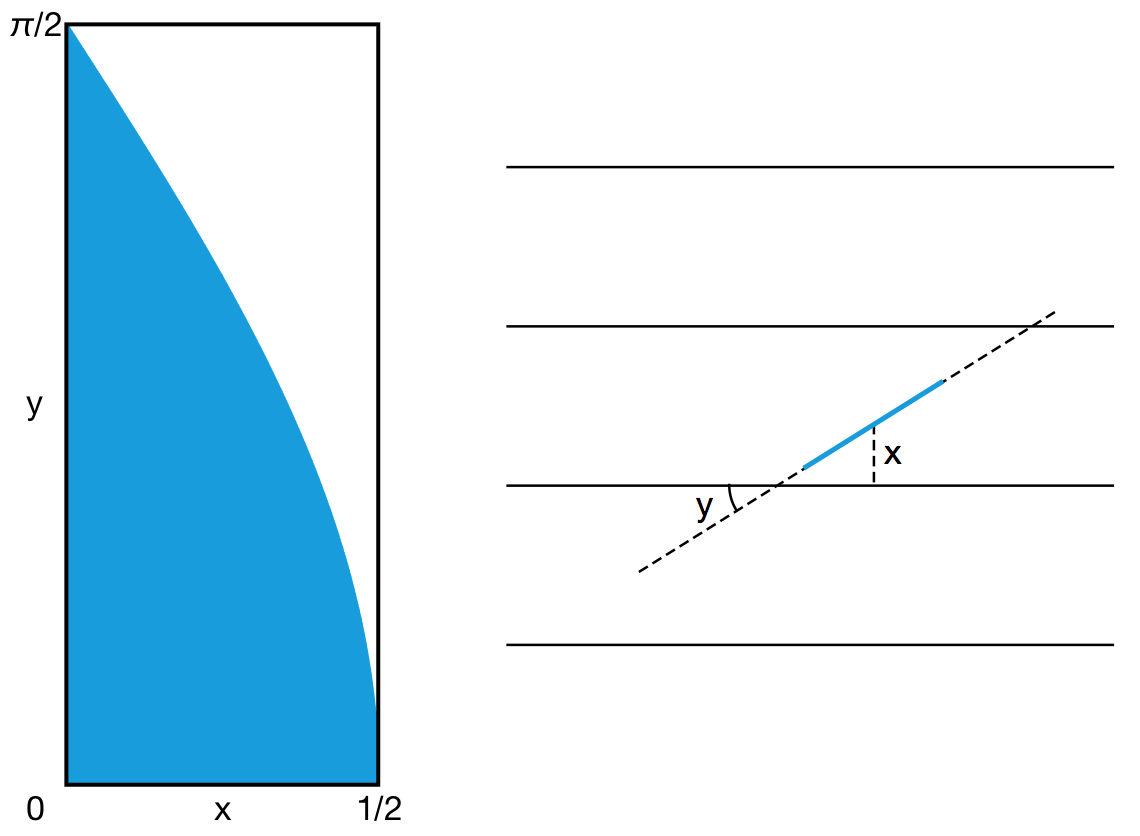
高中數學課本把這種解決概率問題的模型叫做“幾何概型”。說到幾何概型，最經典的可能要算下面這個例題。A 、 B 兩人約定好晚上6:00 到7:00 之間在公園門口見面。每個人都會從6:00 到7:00 這段時間當中隨機挑選一個時間，並在這個時間到達公園門口。每個人都只願意等待15 分鐘，也就是說，如果15 分鐘之後沒有看見對方，那麼就立即離開。那麼，兩人最終能見面的概率有多大？答案是7/16 。

8．圓周上均勻分佈著100 個點。隨便選擇兩個點連一條線段，再隨便選擇另外兩個點連一條線段。那麼，下面哪種情況的可能性更大一些？

A．兩條線段相交
B．兩條線段不相交
C．上述兩種情況的出現概率相同

這個題目的答案是B 。隨便選擇兩個點，再隨便選擇另外兩個點，本質上相當於先隨便選擇四個點，再決定把這四個點配成怎樣的兩對。對於任意四個點A 、 B 、 C 、 D （在圓周上按此順序排列）來說，我們都有三種不同的配對方案：① A – B, C – D ② A – C, B – D ③ A – D, B – C 。其中，只有方案② 對應的兩條連線才會相交。因此，兩條線段相交的概率是1/3 。

9．不透明的盒子裡有1000 張紙條，上面分別寫有1, 2, 3, …, 1000。A 從盒子裡隨機取出100 張紙條，並把這100 張紙條上的數從小到大排成一排。然後， B 從盒子裡剩下的紙條中隨機取出1 張紙條，並看看這張紙條上的數在A 那裡排第幾位。例如，如果A 手中的數有50 個比B 取出的大，另外50 個比B 取出的小，那麼B 手中的數就排第51 位。那麼，下面哪種情況的可能性更大一些？

A．B手中的數排第1位
B．B手中的數排第51位
C．上述兩種情況的出現概率相同

很多人的直覺都是，排第1 可能性不大，排中間可能性更大。而實際上，考慮所有101 個數的101! 種排列方案，或者從1000 個數里選101 個數所產生的P(1000, 101) 種排列方案， B 選的那個數將會等可能地出現在各個位置。因此，這個題目的答案是C 。

如果你還想不明白的話，你乾脆直接想成是， A 抽了100 個數，然後再幫B 抽了一個數，問幫B 抽的這個數更有可能排第幾。如果你還想不明白的話，你乾脆直接想成是， A 抽了101 個數，問最後抽出的這個數更有可能排第幾。如果你還想不明白的話，你乾脆直接想成是， A 選了101 個數往空中一撒，問最後一個落地的數更有可能是排第幾的數。

10．把一副洗好的牌（共52 張）背面朝上地摞成一摞，然後依次翻開每一張牌，直到翻出第一張A 。那麼，下面哪種情況的可能性更大一些？

A．翻開第3張牌時出現了第一張A 
B．翻開第4張牌時出現了第一張A 
C．上述兩種情況的出現概率相同

這個題目的答案是A 。這個答案並不出人意料。你不妨考慮一個非常極端的情況：假設一副牌裡只有三張牌，其中兩張是A ，另外一張是2 。那麼，洗好牌後，三張牌的順序有AA2, A2A, 2AA三種（如果把兩張A看作是兩張不同的A ，那麼三張牌的順序有A 1 A 2 2, A 2 A 1 2, A 1 2A 2 , A 2 2A 1 , 2A 1 A 2 , 2A 2 A 1六種）。翻到第1, 2, 3張牌時出現第一張A的概率分別是2/3, 1/3, 0 。

至於原題為什麼選A ，我們給出一個這樣的解釋。洗好牌後，從前往後四張A 所在的位置一共有C(52, 4) 種可能的情況，分別為(1, 2, 3, 4), (1, 2, 3, 5), ( 1, 2, 3, 6), …, (49, 50, 51, 52) 。其中，形如(3, ?, ?, ?) 的情況顯然比形如(4, ?, ?, ?) 的情況更多，因為前者的問號處可以有更豐富的取值。

11．把一副洗好的牌（共52 張）背面朝上地摞成一摞，然後依次翻開每一張牌，直到翻出第一張A 。那麼，下面哪種情況的可能性更大一些？

A．再下一張牌是黑桃A 
B．再下一張牌是黑桃2 
C．上述兩種情況的出現概率相同

很多人可能會認為，下一張牌是黑桃2 的可能性更大，因為剛才翻出的首張A 可能就是黑桃A 。其實這種直覺是錯誤的。令人吃驚的是，這道題的答案是C 。下一張牌是黑桃A 的概率與下一張牌是黑桃2 的概率一樣大，它們都等於1/52 。

為了說明這一點，我們不妨來看一種同樣能實現絕對隨機的另類洗牌方式：先把一副牌中的黑桃A 抽出來，隨機洗牌打亂剩下51 張牌的順序，然後把黑桃A 插回這摞牌中（包括最頂端和最底端在內，共有52 個可以插入的位置）。顯然，黑桃A 正好插到了這摞牌的首張A 下面有1/52 的可能性。根據同樣的道理，首張A 下面是黑桃2 的概率也是1/52 。事實上，任何一張牌都有可能出現在首張A 的下面，它們出現的概率是相等的，都等於1/52 。

12．把一副洗好的牌（共52 張）背面朝上地摞成一摞。翻開最上面的那張牌，記住這張牌是什麼顏色（紅色還是黑色），然後將它背面朝上地放回原處。隨機切一次牌（即把撲克牌隨機分成上下兩摞，把下面這摞牌疊在上面這摞牌的上面），然後再次翻開最上面的那張牌，記住這張牌是什麼顏色（紅色還是黑色）。那麼，下面哪種情況的可能性更大一些？

A．兩次看到的牌的顏色相同
B．兩次看到的牌的顏色不同
C．上述兩種情況的出現概率相同

答案很簡單：選B 。這是因為，切了一次牌之後，你剛才翻開的那張牌就不可能在最上面了。換句話說，再次翻開的牌將會等可能地是剩餘的51 張牌中的任何一張，其中有26 張牌和你第一次翻開的牌顏色不同，但只有25 張牌和你第一次翻開的牌顏色相同。

13．同時拋擲10 枚硬幣，出現下面哪種情況的可能性更大一些？

A．正面朝上的硬幣數量為偶數
B．正面朝上的硬幣數量為奇數
C．上述兩種情況的出現概率相同

答案是C 。事實上，把10 換成任意正整數，這個問題的答案都不會變——正面朝上的硬幣個數是奇是偶的概率一樣大。

讓我們把這個問題先修改一下：同時拋擲5 枚硬幣，正面朝上的硬幣數量為偶數的概率大，還是為奇數的概率大？有趣的是，新的問題突然有了一種非常簡單的解法。我們可以把同時拋擲5 枚硬幣的結果分成六大類： 0 個正面5 個反面、 1 個正面4 個反面、 2 個正面3 個反面、 3 個正面2 個反面、 4 個正面1 個反面、 5 個正面0 個反面。我們把這六類情況分成三組：

• 0 正5 反， 5 正0 反
• 2 正3 反， 3 正2 反
• 4 正1 反， 1 正4 反

注意到，每一組裡的前後兩類情況出現的概率總是相同的，然而前面那類總是屬於有偶數個正面的情況，後面那類總是屬於有奇數個正面的情況。因而總的來說，有偶數個正面的情況和有奇數個正面的情況將會概率均等地出現。

回到原問題。如果是10 枚硬幣的話，又該怎麼辦呢？大家或許想要故技重施，但卻發現這回不管用了。雖然0 正10 反和10 正0 反出現的概率仍然相等，但它們都是有偶數個正面的情況，這樣就沒法推出奇偶兩種情況各佔一半的結論了。不過，我們另有奇招。把這10 枚硬幣分成兩組，每一組各有5 枚硬幣。根據剛才的結論，每組硬幣裡面出現偶數個正面和出現奇數個正面的概率是相同的，因而，同時拋擲這兩組硬幣後，檢查兩組硬幣正面朝上的數量分別有多少，會產生“偶偶”、“偶奇”、“奇偶”、“奇奇”這四種等概率的組合。在第一種情況和最後一種情況中，最終正面朝上的硬幣數量為偶數；在第二種情況和第三種情況中，最終正面朝上的硬幣數量為奇數。可以看到，正面朝上的硬幣數量是奇是偶的概率相等。

我們還有另一種更簡單的方法來說明，同時拋擲10 枚硬幣後，正面朝上的硬幣數量是奇是偶的概率的確相同。假設你已經拋擲了9 枚硬幣，正準備拋擲最後一枚硬幣。不管前9 枚硬幣拋擲成啥樣，最後這枚硬幣的正反都將會起到決定性的作用，具體情況分為兩種，視前9 枚硬幣的拋擲結果而定：

• 如果最後一枚硬幣是正面，總的正面個數就是偶數；如果最後一枚硬幣是反面，總的正面個數就是奇數；
• 如果最後一枚硬幣是正面，總的正面個數就是奇數；如果最後一枚硬幣是反面，總的正面個數就是偶數。

容易看出，不管是上述兩種情況中的哪種情況，總的正面個數是奇是偶的概率都是相等的。因此，即使上述兩種情況出現的概率不相等（當然，事實上是相等的），最終總的正面個數是奇是偶的概率也是相等的。

14．A 、 B 兩人在玩擲硬幣遊戲，每個人都拋擲10 次硬幣，最後誰拋出的正面更多，誰就獲勝。幾輪遊戲下來後， A 都獲勝了， B 有些沮喪。A 說：“要不這樣吧，我們把遊戲規則改一下。我允許你多拋擲一次硬幣。也就是說，我仍然拋擲10 次硬幣，你卻能拋擲11 次硬幣。但是，只有你拋擲出的正面次數嚴格大於我拋擲出的正面次數，才算你獲勝；如果我們拋擲出的正面次數相同，那也算我獲勝。”新的一輪遊戲開始了，按照約定， A 拋擲了10 次硬幣， B 拋擲了11 次硬幣。理論上，下面哪種情況的可能性更大一些？

A．A獲得遊戲的勝利
B．B獲得遊戲的勝利
C．上述兩種情況的出現概率相同

題目的答案是C 。這是一個非常經典的問題，解決它的方法也有很多。我們介紹兩種方法。

第一種方法如下。在新版遊戲中，假設兩人各自都已經拋擲了10 次硬幣，只待B 拋擲最後一次了。此時，如果B 的正面更多，那他就勝定了，遊戲可以提前結束了。如果B 的正面更少，那他就輸定了，遊戲也可以提前結束了。顯然，這兩種情況出現的概率相同。現在，只剩一種情況有待分析，即此時B 的正面數量與A 相同。那麼，遊戲結果將完全取決於B 的最後一次拋擲：如果B 拋擲出正面，勝；如果B 拋擲出反面，敗。而這兩種情況出現的概率也是相同的。綜上所述，新的遊戲是公平的。

第二種方法如下。既然B 比A 多拋擲一次，那這就說明， B 的正面和反面不可能都沒A 多（否則B 的硬幣總數不可能比A 多）。另外，由於B 只比A 多拋擲一次，那這就說明， B 的正面和反面不可能都比A 多（否則B 的硬幣總數至少比A 大2 ）。綜上所述，要么B 的正面比A 更多，要么B 的反面比A 更多。由於硬幣本身是公正的，因此這兩種情況出現的機率相等，它們各為1/2 。但是， B 的正面比A 更多就意味著B 獲勝了， B 的反面比A 更多就意味著B 的正面數量不比A 多，即A 獲勝了（別忘了，平局算A 獲勝）。所以，兩人各自獲勝的概率都是1/2 。

15．魔術師把一枚正常的硬幣展示給觀眾看，然後說：“接下來，我會拋擲這枚硬幣，每次它都將正面朝上。”觀眾聽聞後議論紛紛，魔術師趁機迅速地把這枚正常的硬幣換成了一枚兩面都是正面的硬幣。魔術師連擲10 次硬幣，次次正面朝上，贏得觀眾雷鳴般的掌聲。其中一個觀眾不服氣地說：“該不會你趁我們不注意，把硬幣換成了兩面都是正面的特殊硬幣吧！如果你有本事的話，你給我們擲出一個'正反正反… …'的序列出來！”為了保住自己的顏面，魔術師只好把那枚正常的硬幣變回手中，硬著頭皮開始拋擲硬幣。倘若魔術師拋擲硬幣沒有任何技巧，每次是正是反的概率相同，那麼魔術師無限地拋擲下去，第一次出錯更有可能出在什麼地方？

A．該擲正面的時候擲出了反面
B．該擲反面的時候擲出了正面
C．上述兩種情況的出現概率相同

這個題目的答案是A 。下面我們證明，因為該擲反面的時候擲出了正面而掛掉的概率，也就是在第偶數次拋擲時掛掉的概率，精確地等於1/3 。容易得出，第2次就掛了的概率就是前2次精確地擲出“正正”序列的概率，它等於1 / 2 2。類似地，到第4次才掛的概率就是前4次精確地擲出“正反正正”序列的概率，它等於1 / 2 4；而到第6次才掛的概率則是前6次精確地擲出“正反正反正正”序列的概率，它等於1 / 2 6 ……所以，在第偶數次掛掉的概率是：

  1 / 2 2 + 1 / 2 4 + 1 / 2 6 + 1 / 2 8 + … 
= 1 / 4 + 1 / 4 2 + 1 / 4 3 + 1 / 4 4 + … 
= (1 + 1 / 4 + 1 / 4 2 + 1 / 4 3 + 1 / 4 4 + …) – 1 
= 1 / (1 – 1 / 4) – 1 
= 1 / 3

倒數第二步用到了無窮等比級數的求和公式（見本文中的第4 題）。

其實，這個答案有一個非常直觀的解釋。想像A 、 B 兩人玩一個擲硬幣遊戲。兩人輪流拋擲硬幣，但A 必須擲出正面， B 必須擲出反面，誰擲錯了誰就立即輸掉遊戲。如果A 先拋硬幣，誰輸掉的概率更大？那當然是A 輸掉的概率更大，因為他先擲嘛！

事實上，設A 輸掉的概率為p ，我們可以巧妙地求出p 來。怎樣的情況下A 才會輸掉呢？如果A 第一次就擲錯了，他就直接輸了，這有1/2 的概率。如果A 第一次擲對了，那麼B 必須也跟著擲對，走到這一步有(1/2) × (1/2) = 1/4 的概率。此時，遊戲又回到了出發點， A 輸掉的概率又變回了p 。於是，我們得到：

p = 1/2 + (1/4) · p

把它當作一個關於p 的一元一次方程，解得p = 2/3 。這就是我們想要的答案。我們將會在很後面的幾個題目裡繼續用到這種技巧。

我們還有一種非常帥的方法來說明，為什麼魔術師首次出錯更容易錯在把正面擲成了反面。把正面看作數字1 ，反面看作數字0 ，那麼觀眾要求的目標序列就變成了101010… 。如果在前面加一個小數點，這就變成了一個0 到1 之間的二進制小數0.101010… ，它等於十進制中的2/3 。而魔術師拋擲的硬幣序列，則構成了一個0 到1 之間的隨機數。如果某一次把0 擲成了1 ，就說明擲出的是一個比2/3 更大的數；如果某一次把1 擲成了0 ，就說明擲出的是一個比2/3 更小的數。顯然，前者的概率是1/3 ，後者的概率是2/3 。

你意識到了嗎？我們相當於用一枚公正的硬幣，模擬出了一枚不公正的硬幣。如果你想要一枚硬幣，它有2/3 的概率正面朝上，有1/3 的概率反面朝上，但你手中只有一枚公正的硬幣，你該怎麼辦呢？你可以像剛才那樣，不斷拋擲硬幣，得出一個0 到1 之間的隨機二進制小數。一旦發現這個二進制小數小於2/3 ，就視最終結果為“正”；一旦發現這個二進制小數大於2/3 ，就視最終結果為“反”。

當然，模擬這樣一枚不公正的硬幣，其實遠不需要這麼麻煩。我們可以連續拋擲2 次硬幣，拋出“正反”或者“反正”都視最終結果為“正”，拋出“正正”則視最終結果為“反”，拋出“反反”則此輪拋擲作廢，重頭再來。這種“分類討論法”能成的原因是， 2/3 是一個有理數。如果我們要模擬一枚不公正的硬幣，它有1 / π 的概率正面朝上，有1 – 1 / π 的概率反面朝上呢？此時，“分類討論法”就不管用了。但是，剛才的“二進制小數法”依舊有效。不斷拋擲硬幣並記錄拋擲結果， 1 代表正面， 0 代表反面，直至某次擲出的結果與1 / π 的二進制小數不符。如果是1 被擲成0 了，則視最終結果為“正”；如果是0 被擲成1 了，則視最終結果為“反”。

如何用一種硬幣去模擬另一種硬幣，這是一個非常有趣的話題，裡面大有文章可作。比方說，我們完全可以提出一個和剛才的問題正好相反的問題：如果你手裡有一枚不公正的硬幣（你不知道它的正反兩面朝上的概率各是多少，你甚至不知道它的哪一面朝上的概率更大），如何才能把它當作一枚公正的硬幣來使？辦法有很多。比方說，考慮連續拋擲兩次硬幣後的結果：如果結果是一正一反，那麼先正後反和先反後正的概率一定是相同的（即使這枚硬幣是不公平的）。借助這一點，我們就有了下面這個方案：連續拋擲兩次硬幣，如果兩次拋擲的結果是“正反”，就視最終結果為“正”；如果兩次拋擲的結果是“反正”，就視最終結果為“反”；如果是其他情況，就重新再來。

如果把兩種甚至更多種不同的硬幣組合起來使用，在某些限制條件下模擬出某些特定的概率事件，這裡面的水就更深了。這裡有一個與此相關的問題，感興趣的話不妨去看看：http://www.matrix67.com/blog/archives/6151。

16．A 、 B 兩人為一件小事爭執不休，最後決定用拋擲硬幣的辦法來判斷誰對誰錯。不過，為了讓遊戲過程更刺激，兩人決定採用這樣一種方案：連續拋擲硬幣，直到最近三次硬幣拋擲結果是“正反反”或者“反反正”。如果是前者，那麼A 獲勝；如果是後者，那麼B 獲勝。理論上，下面哪種情況的可能性更大一些？

A．A獲得遊戲的勝利
B．B獲得遊戲的勝利
C．上述兩種情況的出現概率相同

乍看上去， B 似乎沒有什麼不同意這種玩法的理由，畢竟“正反反”和“反反正”的概率是均等的。連續拋擲三次硬幣可以產生8 種不同的結果，上述兩種各佔其中的1/8 。況且，序列“正反反”和“反反正”看上去又是如此對稱，獲勝概率怎麼看怎麼一樣。

不過，實際情況究竟如何呢？實際情況是，這個遊戲並不是公平的—— A 的獲勝概率是B 的3 倍！雖然“正反反”和“反反正”在一串隨機硬幣正反序列中出現的頻率理論上是相同的，但別忘了這兩個序列之間有一個競爭的關係，它們要比賽看誰先出現。一旦拋擲硬幣產生出了其中一種序列，遊戲即宣告結束。這樣一來， B 就處於了一個非常窘迫的位置：不管什麼時候，只要擲出了一個正面，如果B 沒贏的話， B 就贏不了了——在出現“反反正”之前， A 的“正反反”必然會先出現。

事實上，整個遊戲的前兩次硬幣拋擲結果就已經決定了兩人最終的命運。只要前兩次拋擲結果是“正正”、“正反”、“反正”中的一個， A 都必勝無疑， B 完全沒有翻身的機會；只有前兩次擲出的是“反反”的結果， B 才會贏得遊戲的勝利。因此， A 、 B 兩人的獲勝概率是三比一， A 的優勢絕不止是一點。所以說，這道題目的正確選項為A 。

這裡有對此遊戲更加深入的討論：http://www.matrix67.com/blog/archives/6015。

似乎是還嫌遊戲雙方的勝率差異不夠驚人， 2010 年， Steve Humble 和Yutaka Nishiyama 提出了上述遊戲的一個加強版。去掉一副撲克牌中的大小王，洗好剩下的52 張牌後，一張一張翻開。一旦出現連續三張牌，花色依次是紅黑黑，那麼玩家A 加一分，同時把翻開了的牌都丟掉，繼續一張張翻沒翻開的牌；類似地，一旦出現連續三張牌恰好是黑黑紅，則玩家B 得一分，棄掉已翻開的牌後繼續。

容易看到，加強版遊戲相當於是重複多次的擲硬幣遊戲，因而毫無疑問，在這個新遊戲中，玩家A 的優勢還會進一步放大。電腦計算顯示， A 獲勝的概率高達93.54% ， B 獲勝的概率則只有可憐的2.62% 。另外3.84% 則是兩人平手的概率。然而，即使是這樣，這個遊戲看上去也會給人一種公平的錯覺！

這個例子告訴我們，在賭博遊戲中，直覺並不是準確的，求助概率論是很有必要的。

其實，概率論的誕生本來就和賭博遊戲是緊緊聯繫在一起的。提到概率論的誕生，不得不提一位名叫Antoine Gombaud 的法國作家。這人出生於1607 年法國西部​​的一個小城市，他並不是貴族出身，但他卻有著“騎士”的光輝頭銜——不過那隻是他自封的而已。他借用了一個自己筆下的人物形象名稱，自封為de Méré 騎士。後來，這個名字便逐漸取代了他的真名Antoine Gombaud 。不過， de Méré 騎士並沒有憑藉自己的文學作品名揚天下，真正讓他聲名遠揚的是他的賭博才能。而足以讓他在歷史上留名的，則是他對一個賭博遊戲的思考。

在17 世紀，法國賭徒間流行著一個賭博遊戲：連續拋擲一顆骰子4 次，賭裡面是否會出現至少一個6 點。這個遊戲一直被視為是一個公平的賭博遊戲，直到1650 年左右， de Méré 在另一個類似的遊戲中莫名其妙地輸得四個荷包一樣重。當時， de Méré 參加了這個賭博遊戲的一個“升級版”：把兩顆骰子連續拋擲24 次，賭是否會擲出一對6 點來。

de Méré 自己做了一番思考。同時拋擲兩顆骰子出現一對6 ，比拋擲一顆骰子出現6 點要困難得多，前者的概率是後者的1/6 。要想彌補這個減小了的概率，我們應當把兩顆骰子連續拋擲6 次。為了追上連續拋擲4 次骰子出現一個6 的概率，則應當把兩顆骰子拋擲24 次才行。de Méré 果斷地得出結論：在升級版遊戲中出現一對6 的概率，與傳統遊戲中出現一個6 的概率是相等的，升級版遊戲換湯不換藥，與原來的遊戲本質完全一樣。

不過，這畢竟是不嚴格的直覺思維，事實情況如何還得看實戰。在以前的遊戲中， de Méré 總是賭“會出現6 點”，經驗告訴他這能給他帶來一些細微的優勢。於是這一回， de Méré 也不斷押“會出現一對6”。不料，這次他卻賠得多賺得少，最終輸了個精光。

這是怎麼一回事兒呢？作為一個業餘數學家， de Méré 感到裡面有玄機。但是，憑藉自己的數學知識，他沒有能力解決這個難題。無奈之下，他只好求助當時的大數學家Blaise Pascal 。

Pascal 可是真資格的數學家。他很快便意識到，這種問題的計算不能想當然，事實和直覺的出入可能會相當大。比方說， de Méré 的直覺就是有問題的：重複多次嘗試確實能增大概率，但這並不是成倍地增加。拋擲一顆骰子出現6 點的概率為1/6 ，但這並不意味著拋擲骰子4 次會出現一個6 點的概率就是1/6 的4 倍。無妨想一個更極端的例子：按此邏輯，拋擲一顆骰子6 次，出現至少一次6 點的概率似乎就該是6/6 ，也即100% ，但這顯然是不對的。如果拋擲骰子6 次以上，出現一個6 點的概率就會超過100% ，這就更荒謬了。

看來，概率不能簡單地加加減減，每一步推理都要有憑有據。Pascal 考慮了遊戲中所有可能出現的情況，算出了在新舊兩種版本的遊戲中，會出現一個（或一對） 6 點的概率分別是多少。

連續拋擲4次骰子，總共會產生6 4，也就是1296種可能。不過在這裡面，一個6點都沒有的情況共有5 4，也就是625種。反過來，至少有一個6點就有1296 – 625 = 671種情況，它佔所有情況的671 / 1296 ≈ 51.77% ，恰好比50%高出那麼一點點。看來， de Méré的經驗是對的——眾人公認的公平遊戲並不公平，賭6點會出現確實能讓他有機可乘。

那麼，連續拋擲兩顆骰子24次，能出現一對6的概率又是多少呢？這回計算的工程量就有點大了。兩顆骰子的點數有36種組合，連拋24次則會有36 24，大約是2.245 × 10 37種情況。而24次拋擲中，從沒產生過一對6點的情況數則為35 24，大約為1.142 × 10 37。可以算出，如果賭24次拋擲裡會出現一對6 ，獲勝的概率是49.14% 。又一個非常接近50%的數，只不過這次是比它稍小一些。

原來，升級版遊戲並不是換湯不換藥。兩種遊戲勝率雖然接近，但正好分居50% 兩邊。這看似微不足道的差別，竟害得我們的“騎士”馬失前蹄。

後來，這個經典的概率問題就被命名為“de Méré 問題”。在解決這個問題的過程中， Pascal 提出了不少概率的基本原理。因此， de Méré 問題常被認為是概率論的起源。

當然， de Méré 的故事多少都有一些杜撰的成分，大家或許會開始懷疑，在現今世界裡，有沒有什麼還能玩得到的“偽公平遊戲”呢？答案是肯定的。為了吸引玩家，賭場想盡各種花樣精心設計了一個個迷魂陣一般的賭局。在那些最流行的賭博遊戲中，莊家一方總是會稍佔便宜；但遊戲規則設計得如此之巧妙，以至於乍看上去整個遊戲是完全公平，甚至是對玩家更有利的。“骰子擲好運”（chuck-a-luck）便是一例。

“骰子擲好運”的規則看上去非常誘人。每局遊戲開始前，玩家選擇1 到6 之間的一個數，並下1 塊錢的賭注。然後，莊家同時拋擲三顆骰子。如果這三顆骰子中都沒有你選的數，你將輸掉那1 塊錢；如果有一顆骰子的點數是你選的數，那麼你不但能收回你的賭注，還能反贏1 塊錢；如果你選的數出現了兩次，你將反贏2 塊錢；如果三顆骰子的點數都是你選的數，你將反贏3 塊錢。用賭博的行話來說，你所押的數出現了一次、兩次或者三次，對應的賠率分別是1:1 、 1:2 、 1:3 。

用於拋擲三顆骰子的裝置很有創意。它是一個沙漏形的小鐵籠子，三顆骰子已經預先裝進了這個籠子裡。莊家“拋擲”骰子，就只需要把整個沙漏來個180 度大迴旋，倒立過來放置即可。因此，“骰子擲好運”還有一個別名——“鳥籠”（birdcage）。

18 世紀英國皇家海軍的水手間流行過一種叫做“皇冠和船錨”（Crown and Anchor）的賭博遊戲，其規則與“骰子擲好運”一模一樣。唯一不同之處只是骰子而已。普通骰子的六個面分別是1 點到6 點，而“皇冠和船錨”所用骰子的六個面則是六種不同的圖案——撲克牌的黑、紅、梅、方，再加上皇冠和船錨兩種圖案。之後，“賭博風”又蔓延到了商船和漁船上，“皇冠和船錨”也就逐漸走出了皇家海軍的圈子。一般認為，這也就是“骰子擲好運”的起源了。現在，很多賭場都提供了“骰子擲好運”的賭博項目。

對玩家而言，這個遊戲看上去簡直是在白送錢：用三顆骰子擲出6個數中的一個，怎麼也會有一半的概率砸中吧，那玩家起碼有一半的時間是在賺錢，應當是穩賺不賠呀。其實，這是犯了和de Méré一樣的錯誤——一顆骰子擲出玩家押的數有1/6的概率，並不意味著三顆骰子同時拋擲就會有3/6的概率出現此數。在拋擲三顆骰子產生的所有6 3種情況中，玩家押的數一次沒出現有5 3種情況，所佔比例大約是57.87% 。也就是說，大多數時候玩家都是在賠錢的。

不過，考慮到賺錢時玩家有機會成倍地贏錢，這能否把輸掉的錢贏回來呢？一些更為細緻的計算可以告訴我們，即使考慮到這一點，遊戲對玩家仍然是不利的：平均每賭1 塊錢就會讓玩家損失大約8 分錢。不過，我們還有另一種巧妙的方法，無需計算便可看出這個遊戲對玩家是不利的。

這顯然是一個沒有任何技巧的賭博遊戲，不管押什麼勝率都是一樣的。因此，不妨假設有6 名玩家同時在玩這個遊戲，這6 個人分別賭6 個不同的點數。此時玩家聯盟的輸贏也就足以代表單個玩家的輸贏了。

假設每個人都只下注1 塊錢。拋擲骰子後，如果三顆骰子的點數都不一樣，莊家將會從完全沒猜中點數的三個人手中各賺1 塊，但同時也會賠給另外三人各1 塊錢；如果有兩顆骰子點數一樣，莊家會從沒猜中點數的四個人那裡贏得共4 塊，但會輸給另外兩人3 塊；如果三顆骰子的點數全一樣，莊家則會贏5 塊但虧3 塊。也就是說，無論拋擲骰子的結果如何，莊家都不會賠錢！雖然一輪遊戲下來有的玩家賺了，有的玩家虧了，但從整體來看這6 名玩家是在賠錢的，因此平均下來每個玩家也是在不斷輸錢的。

17．同時拋擲6 顆骰子，出現下面哪種情況的可能性更大一些？

A．不同數字的個數恰好為4個
B．不同數字的個數為1 、 2 、 3 、 5或6個
C．上述兩種情況的出現概率相同

這個題目的答案竟然是A ，沒想到吧！賭博遊戲的勝率常常違反直覺，這道題目又是一個經典的例子。同時拋擲6顆骰子，一共會產生6 6 = 46656種情況。其中，不同數字的個數恰好為4個的情況有多少種呢？如果6顆骰子裡只有4個不同的數字，那麼有的數字出現了至少2次。事實上，各個數字出現的次數只有以下兩種可能的分佈類型：

• 其中1 個數字出現了3 次，另外3 個數字各出現了1 次
• 其中2 個數字各出現了2 次，另外2 個數字各出現了1 次。

前者一共有C(6, 3) × C(6, 4) × 4! = 7200 種具體的情況，其中C(6, 3) 表示出現了3 次的數字究竟出現在了哪3 次， C( 6, 4) 表示這4 個數字究竟是哪4 個數字。後者一共有C(6, 2) × C(4, 2) × C(6, 4) × 4! / 2 = 16200 種具體的情況，其中C(6, 2) 表示第一個出現了2次的數字究竟出現在了哪2 次， C(4, 2) 表示第二個出現了2 次的數字究竟出現在了哪2 次， C(6, 4) 表示這4 個數字究竟是哪4個數字，最後的結果除以2 的原因是，第一個出現了2 次的數和第二個出現了2 次的數有可能分別是我和你，也有可能分別是你和我，這被算重了。

因此，不同數字的個數恰好為4 個的情況一共有7200 + 16200 = 23400 種，它佔總數的23400 / 46656 ≈ 50.154321% 。

18．小明走進一家賭場，來到了輪盤賭跟前。輪盤賭的轉盤上有38 個格子，上面分別標著0, 00, 1, 2, 3, …, 36 。遊戲開始後，一個白色小球會逆著輪盤旋轉的方向滾動，最終等概率地落入38 個格子中的一個。小明每次可以在任意一個格子上下1 元的賭注。如果小球落入了小明所選的格子裡，則小明贏得36 元（但那1 元錢的賭注仍然歸賭場）；如果小球落入了別的格子裡，則小明什麼也得不到（那1 元也就打水漂了）。小明身上只有105 元錢，於是，他連續賭了105 次。那麼，下面哪種情況的可能性更大一些？

A．小明賺著離開了賭場
B．小明虧著離開了賭場
C．上述兩種情況的出現概率相同

花1 元賭某一個格子，中籤的概率是1/38 ，但卻只能贏來36 元。毫無疑問，輪盤賭是一個赤裸裸的對賭場更有利的賭博遊戲。所以，這道題應該選B 咯？不對！這道題的正確答案其實是A 。在這道題中， 105 這個數起到了比較關鍵的作用。讓我們來實際計算一下。

由於每贏一次會得到36元，因此小明只需要贏3次或3次以上，便能實現賺著離開賭場了。小明一次沒贏的概率為(37/38) 105 ≈ 0.0608 ，恰好贏1次的概率為C(105, 1) × (1/38) × (37/38) 104≈ 0.1725 ，恰好贏2次的概率為C(105, 2) × (1/38) 2 × (37/38) 103 ≈ 0.2425 ，上述三個值加起來約為0.4758 。所以，反過來，小明贏了3次或3次以上的概率就是0.5242 ，這超過了1/2 。

為什麼在玩一個明顯對賭場更有利的賭博遊戲中，精確地花費105 元錢，就能做到賺時多虧時少？如果每個人都這麼做，賭場豈不是會被搞垮？這不跟遊戲對賭場更有利的結論相矛盾嗎？其實，賺的時候更多，並不意味著期望收益為正。雖然賺的時候多，虧的時候少，但賺的時候往往是賺小錢，虧的時候往往是虧大錢，平均算下來，玩家仍然是在不斷送錢的。

19．法國有法國的輪盤賭，俄羅斯也有俄羅斯的輪盤賭。不過，戰鬥民族的賭博方式可不一樣——不是賭錢，而是賭命。俄羅斯輪盤賭可謂是史上最酷的決斗方式。左輪手槍的轉輪中有六個彈槽。在其中一個彈槽中放入一顆子彈，然後快速旋轉轉輪，再把它合上。參與決鬥的兩個人輪流對準自己的頭部扣動扳機，直到其中一方死亡。這是一場真男人遊戲，雙方勝負的概率各佔50% ，遊戲沒有任何技巧可言，命運決定了一切。為了讓遊戲更加刺激，這一回我們稍微改變一下游戲規則。在轉輪的連續三個彈槽中放入子彈，然後旋轉並合上轉輪。這一次，理論上，下面哪種情況的可能性更大一些？

A．先開槍的人死亡
B．後開槍的人死亡
C．上述兩種情況的出現概率相同

或許有些出人意料的是，這個題目的答案為A 。為了算出雙方存活的概率，我們只需要考慮所有6 種可能的子彈位置即可。不妨用符號⊙ 來表示有子彈的彈槽，用符號○ 來表示空的彈槽。我們便能列出下面這張表：

• ⊙⊙⊙○○○ → 先開槍者死
• ⊙⊙○○○⊙ → 先開槍者死
• ⊙○○○⊙⊙ → 先開槍者死
• ○○○⊙⊙⊙ → 後開槍者死
• ○○⊙⊙⊙○ → 先開槍者死
• ○⊙⊙⊙○○ → 後開槍者死

可見，先開槍者死亡的概率高達2/3 ，是後開槍者死亡概率的兩倍。

可以算出，當轉輪裡位置相連的子彈數分別為1 、 2 、 3 、 4 、 5 、 6 時，先開槍者死亡的概率分別為1/2 、 2/3 、 2/3 、 5/ 6 、 5/6 、 1 。看來，並不是所有遊戲都是先下手為強啊。

20．小明參加某電視台的選秀節目。A 、 B 、 C 三位導師欣賞了小明的一番激情演唱後，需要投票決定小明能否晉級。小明的表演征服了A 、 B 兩位導師，每位導師都有4/5 的概率投出贊成票，支持小明晉級。但C 導師則猶豫不決，不知道該如何選擇。怎麼辦呢？節目組給出了兩種方案供小明選擇。第一種方案是， A 、 B 兩位導師獨立作出決定， C 則拋擲一枚公正的硬幣，如果硬幣正面朝上，則晉級與否完全以A 的決定為準，如果硬幣反面朝上，則晉級與否完全以B 的決定為準。第二種方案是，A 、 B 兩位導師獨立投出贊成票或反對票， C 則拋擲一枚公正的硬幣，如果硬幣正面朝上，則投出贊成票，如果硬幣反面朝上，則投出反對票，最後晉級與否則取決於三人中的多數票。為了提高晉級的概率，小明應該選擇哪種方案？

A．選擇第一種方案
B．選擇第二種方案
C．兩種方案的晉級概率相同

這個題目的答案是C 。兩種方案中，小明晉級的概率是相同的，都是4/5 。即使把題目中4/5這個比例換一換，答案也依舊如此。不妨假設A 、 B兩位導師投出贊成票的概率都是p ，那麼第一種方案中小明晉級的概率顯然是(1/2) · p + (1/2) · p = p 。第二種方案呢？兩位導師都投出贊成票的概率是p 2，此時小明必然晉級； A投出贊成票B投出反對票的概率是p · (1 – p) ，此時小明有1/2的概率晉級（這取決於C ）； A投出反對票B投出贊成票的概率是(1 – p) · p ，此時小明有1/2的概率晉級（這取決於C ）；其他情況下小明都無法晉級。因此，第二種方案中小明晉級的概率為p 2 + (1/2) · p · (1 – p) + (1/2) · (1 – p) · p ，化簡的結果是一樣的： p 。

21．小明上了幾次象棋課，回到家得意地要和爸爸媽媽一比高低。爸爸說：“好啊，那我們來搞一次家庭挑戰賽吧。比賽分三輪進行，爸爸媽媽將會作為你的對手輪番上場。如果你在任意連續的兩輪比賽中獲勝，你就能得到一大筆零花錢。對了，挑戰賽開始前，你可以指定爸爸媽媽的出場順序哦。”小明深知，戰勝爸爸的概率更低，戰勝媽媽的概率更高（事實上也的確如此）。為了提高得到零花錢的概率，小明應該怎樣安排爸爸媽媽的出場順序？

A．爸爸、媽媽、爸爸
B．媽媽、爸爸、媽媽
C．兩種情況下得到零花錢的概率相同

這是一個非常經典的問題。你或許會覺得，方案B 更好，因為小明會更多地面對較弱的對手。而實際上，這個題的答案是A 。這背後有一個很簡單的直覺：中間那個人一定不能太強，因為中間那場輸了，整個兒就沒機會了。

我們可以定量地分析一下。假設戰勝爸爸的概率是p ，戰勝媽媽的概率是q ，根據題目假設， p < q 。如果採用爸爸、媽媽、爸爸的順序，則得到零花錢的概率等於贏了前兩場輸了最後一場的概率，加上贏了後兩場輸了第一場的概率，再加上三場都贏了的概率。最後結果是：

p · q · (1 – p) + (1 – p) · q · p + p · q · p = 2 · p · q – p 2 · q

類似地，如果採用媽媽、爸爸、媽媽的順序，則得到零花錢的概率就是：

q · p · (1 – q) + (1 – q) · p · q + q · p · q = 2 · p · q – p · q 2

由於p < q ，因此前一個式子一定比後一個式子更大。

22．一架客機上有100 個座位， 100 個人排隊依次登機。第一個乘客把登機牌搞丟了，但他仍被允許登機。由於他不知道他的座位在哪兒，他就隨機選了一個座位坐下。以後每一個乘客登機時，如果他自己的座位是空著的，那麼他就在他自己的座位坐下；否則，他就隨機選一個仍然空著的座位坐下。當最後一個人登機時，發生下面哪種情況的可能性更大一些？

A．他發現剩下的空位正好就是他的
B．他發現剩下的空位不是他的
C．上述兩種情況的出現概率相同

你或許會以為情況A 出現的概率很小，但實際上，這個概率是50% 。換句話說，這個題目的答案是C 。我們可以通過一些嚴格而復雜的計算來說明這一點，但在這裡，我更願意給出一些直觀的解釋。注意到，當最後一名乘客登機時，最後一個空位要么就是他的，要么就是第一個乘客的（其他的座位如果沒被別人搶占，最終也會被它真正的主人佔據）。這兩個位置會面對98 個人的選擇，它們的“地位”是相等的，它們的“命運”是相同的，不存在哪個概率大哪個概率小的問題。因此，它們成為最後一個空位的概率是均等的。也就是說，最後一個人發現剩下的空位正好是他的，其概率為50% 。

下面是另一個有趣的解釋。我們可以把問題等價地修改為，如果一個人發現自己的座位被別人佔據後，他就叫這個人重新去找一個位置，自己則在這裡坐下。結果你會發現，真正在飛機上跑來跑去不斷換座位的人其實只有一個，就是第一個人。我們可以乾脆叫他直接站在旁邊，等他後面的98 個人全部入座後，他再選個座位坐下。容易看出，他選中的座位要么是他自己的，要么是最後一個人的，這各佔50% 的概率。因此，最後一個人上來之後，正好能對號入座的概率也就是50% 。

23．在每一代的繁殖中，每個阿米巴原蟲都有2/3 的概率分裂成兩個，有1/3 的概率死亡（而不產生下一代）。初始時只有一個阿米巴原蟲，那麼下面哪種情況的可能性更大一些？

A．阿米巴原蟲在有限代之後滅絕
B．阿米巴原蟲無限地繁殖下去
C．上述兩種情況的出現概率相同

注意到，這個問題是有意義的。阿米巴原蟲要么在有限代之後滅絕，要么無限地繁殖下去。我們的問題就是，究竟發生哪種情況的可能性更大。

實際上，這個題的答案選C 。不妨把一個阿米巴原蟲能無限繁殖下去的概率設為p 。初始時的那個阿米巴原蟲怎樣才能無限繁殖下去呢？首先，它得分裂為兩個阿米巴原蟲，這有2/3 的概率；然後，其中至少一個阿米巴原蟲要無限繁殖下去。於是，我們得到式子：

p = (2/3) · (1 – (1 – p) 2 )

其中， (1 – p) 2表示兩個阿米巴原蟲都沒能無限繁殖下去的概率。把上面的式子當作一個關於p的一元二次方程，可解得p = 0或p = 1/2 。捨去p = 0 ，於是得到p = 1/2 。這就說明， A 、 B兩種情況的出現概率是相同的。

為什麼我們可以捨去p = 0呢？要想說服自己這一點，這還真不容易。下面是一個不嚴謹的思路。如果我們把每個阿米巴原蟲分裂成兩個的概率記作p 0（原題則相當於p 0 = 2/3時的特例），那麼阿米巴原蟲無限繁殖下去的概率p就會滿足：

p = p 0 · (1 – (1 – p) 2 )

解得p = 0或p = (2 · p 0 – 1) / p 0。那麼， p究竟是多少呢？注意到以下三點：

1. 當p 0 = 1時，問題的答案顯然應該為1 ；
2. 不管p 0是多少，問題的答案顯然都應該是正數；
3. 在p 0連續變化的過程中，問題的答案也應該發生連續的變化（這個猜測是合理的，我們姑且假設它正確，不再進行論證）。

為了同時滿足上述三點，只有這樣一種可能：當p 0 = 1/2時，問題的答案為0 ；當p 0 < 1/2時，捨去後面那個解，即問題的答案一直都是0 ；當p 0 > 1/2時，捨去前面那個解，即問題的答案為(2 · p 0 – 1) / p 0。

24．一斤白酒下肚後，我醉醺醺地來到了懸崖邊上。如果我再往前邁一步，就會掉下懸崖。我每過一分鐘都會往前或者往後邁一步，每次有1/3 的概率往前邁一步，有2/3 的概率往後邁一步。假設懸崖邊是一條直線，我每步方向都嚴格垂直於懸崖邊，且步長保持一致。如果我無限地走下去，那麼下面哪種情況的可能性更大一些？

A．我在有限步之後將會掉下懸崖
B．我永遠不會掉下懸崖
C．上述兩種情況的出現概率相同

注意到，這個問題是有意義的。我要么在有限步之後掉下懸崖，要么永遠不會掉下懸崖。我們的問題就是，究竟發生哪種情況的可能性更大。

實際上，這個題的答案也是C 。不妨假設我在有限步之後將會掉下懸崖的概率為p 。那麼， p 等於多少呢？如果我第一步就往前邁，那就直接掉下去了。這有1/3 的概率。在另外2/3 的情況下，我的第一步是往後邁的。如果我最後還是掉下懸崖了，那麼在此期間，我一定回過出發點。回到出發點，本質上就相當於往前淨走一步，這和從出發點出發最終掉下去了一樣，概率都是p ；回到出發點後，要想真的掉下去，這又有一個p 的概率。於是，我們得到：

p = 1/3 + (2/3) · p 2

解得p = 1/2 或p = 1 。捨去p = 1 ，於是得到p = 1/2 。這就說明， A 、 B 兩種情況的出現概率是相同的。

為什麼我們可以捨去p = 1呢？這裡，我們可以使用和上一題類似的思路。如果用p 0代替題目中的2/3 ，則上面的式子變為了：

p = (1 – p 0 ) + p 0 · p 2

解得p = (1 – p 0 ) / p 0或p = 1 。為了保證連續性，當p 0 > 1/2時，我們需要捨去p = 1 。

你或許已經發現了，這一題和上一題非常相似。進一步考察兩個問題的答案，你還會有更驚人的發現：在有限步之後掉下懸崖的概率是(1 – p 0 ) / p 0，因此永遠不會掉下懸崖的概率是1 – ( 1 – p 0 ) / p 0 = (2 · p 0 – 1) / p 0。這正是上一題中阿米巴原蟲無限繁殖下去的概率的表達式。

其實，這兩道題的本質就是完全一樣的。讓我們把阿米巴原蟲數量的變化想像成是數軸上不斷左右移動的點。剛開始，這個點在x = 1 的位置。考慮某個阿米巴原蟲：如果它分裂了，那麼數軸上的點會向右移動一個單位，這有2/3 的概率；如果它死亡了，那麼數軸上的點會向左移動一個單位，這有1/3 的概率。上一題就相當於是問，數軸上的點更有可能會在有限步之後到達x = 0 的位置，還是更有可能永遠都到不了x = 0 的位置。如果你把數軸上的點左移右移想成是在懸崖外前進後退，把x = 0 的位置想像成掉下懸崖的位置，這就瞬間變成這一題的背景了。

25．A 、 B 兩支球隊之間要打100 場比賽。初始時，兩支球隊的經驗值都為1 。在每一場比賽中，兩支球隊各自的獲勝概率與它們的經驗值成正比，隨後獲勝​​一方的經驗值將會加1 。那麼，當100 場比賽全部打完之後，下面哪種情況的可能性更大一些？

A．球隊A在所有100場比賽中全部獲勝
B．球隊A在所有100場比賽中恰好有50場獲勝
C．上述兩種情況的出現概率相同

這是一個強者愈強，弱者愈弱的過程，因此其中一支球隊完胜另一支球隊的概率並不會太低，兩支球隊最終打成平手的概率也並不會太高。事實上，兩種情況發生的概率是相同的，都是1/101 。也就是說，這個題目的答案是C 。

讓我們把A 、 B 兩支球隊打比賽的過程進一步抽象成下面這樣：從字符串AB 出發，不斷選擇某個字母並把它分裂成兩個。也就是說，初始時的字符串為AB ，每一次你需要隨機選擇一個字母，如果選中了A ，就把它變成AA ，如果選中了B ，就把它變成BB 。第一次操作之後， AB 有可能變成AAB ，也有可能變成ABB ；如果第一次操作之後的結果是AAB ，那麼第二次操作之後，結果就會概率均等地變成AAAB 、 AAAB 和AABB之一。容易看出，字母A 、 B 數量增加的模式，與原問題中A 、 B 兩支球隊經驗值增加的模式是完全一致的，因而我們要求的概率值就等價地變為了： 100 次操作之後，字符串變成AAA…AAB 的概率是多少，字符串變成AA…AABB…BB （兩種字母各半）的概率又是多少。下面我們來說明，這兩個概率值都是1/101 。

先來看一個似乎與此無關的東西：把0 到100 之間的數隨機排成一行的另類方法。首先，在紙上寫下數字0 ；然後，把數字1 寫在數字0 的左邊或者右邊；然後，把數字2 寫在最左邊，最右邊，或者0 和1 之間……總之，把數字k概率均等地放進由前面k 個數產生的（包括最左端和最右端在內的）共k + 1 個空位中的一個。寫完100 之後，我們就得到了所有數的一個隨機排列。

現在，讓我們假設初始時的字符串是A 0 B ，並且今後每次分裂時，都在分裂得到的兩個字母之間標註這是第幾次分裂。也就是說，下一步產生的字符串就是A 1 A 0 B或者A 0 B 1 B之一。如果下一步產生的字符串是A 1 A 0 B ，那麼再下一步產生的字符串就會是A 2 A 1 A 0 B 、 A 1A 2 A 0 B 、 A 1 A 0 B 2 B之一……聯想前面的討論，你會發現，第100次操作結束後，所有數字實際上形成了一個0到100的隨機排列，也就是說最開始的數字0最後出現在各個位置的概率是均等的。因此，最右邊那個位置上的數字就是0的概率是1/101 ，正中間那個位置上的數字就是0的概率也是1/101 。這其實就是我們要比較的那兩個概率值。

26．從全體正整數中隨機選出兩個正整數，則下面哪種情況的可能性更大一些？

A．這兩個正整數互質（沒有大於1的公約數）
B．這兩個正整數不互質（有大於1的公約數）
C．上述兩種情況的出現概率相同

這個問題的說法很不嚴謹。我們給出一個更加嚴謹的敘述方法。讓我們用P N來表示，從1到N中隨機取出兩個正整數，它們互質的概率是多少。我們的問題就是，當N趨於無窮時， P N的值究竟是大於1/2 ，等於1/2 ，還是小於1/2 。

這是一個非常非常經典的問題。下面是最常見的一種解法。假設我們從全體正整數中隨機選出了兩個正整數a 、 b 。其中， a能被2整除的概率是1/2 ， b能被2整除的概率是1/2 。因而，它們都能被2整除的概率就是1 / 2 2。反過來，它們不都能被2整除的概率就是1 – 1 / 2 2。類似地，它們不都能被3整除的概率就是1 – 1 / 3 2，它們不都能被5整除的概率就是1 – 1 / 5 2 ……於是，它們互質的概率就是：

(1 – 1 / 2 2 ) · (1 – 1 / 3 2 ) · (1 – 1 / 5 2 ) · (1 – 1 / 7 2 ) …

注意，這裡用到了一個假設：如果p 和q 是兩個質數，那麼能否被p 整除和能否被q 整除，這是互相獨立的。事實上也確實如此：一個數能被p 整除的概率是1 / p ，一個數能被q 整除的概率是1 / q ；一個數能同時被兩個質數p 和q 整除，當且僅當它能被p · q 整除，其概率是1 / (p · q)。

為了求出上面這個式子的值，我們考慮它的倒數。1 – 1 / 2 2的倒數是1 / (1 – 1 / 2 2 ) ，而由無窮等比級數的求和公式（見本文中的第4題），它又可以被我們寫成1 + 1 / 2 2 + 1 / 2 4 + 1 / 2 6 + … 。類似地，其他幾項也都變成了1 + 1 / 3 2 + 1 / 3 4 + 1 / 3 6 + … ，1 + 1 / 5 2 + 1 / 5 4 + 1 / 5 6 + … ，等等。現在，想像一下，如果把所有的括號全都展開，把所有的項全都乘開來，會得到什麼？我們會既無遺漏又無重複地得到所有的1 / n 2！

  (1 + 1 / 2 2 + 1 / 2 4 + 1 / 2 6 + … ) · (1 + 1 / 3 2 + 1 / 3 4 + 1 / 3 6 + … ) 
  · (1 + 1 / 5 2 + 1 / 5 4 + 1 / 5 6 + … ) · … 
= 1 + 1 / 2 2 + 1 / 3 2 + 1 / 4 2 + 1 / 5 2 + …

比方說， 40 = 2 × 2 × 2 × 5 ，那麼等式右邊的1 / 40 2這一項，就是由等式左邊的第一個括號裡的1 / 2 6，乘以第二個括號裡的1 ，乘以第三個括號裡的1 / 5 2，乘以其餘所有括號裡的1得到的。

1 + 1 / 2 2 + 1 / 3 2 + 1 / 4 2 + 1 / 5 2 + …究竟等於多少呢？我們來證明，它小於2 。這是因為：

  1 + 1 / 2 2 + 1 / 3 2 + 1 / 4 2 + 1 / 5 2 + … 
< 1 + 1 / (1 × 2) + 1 / (2 × 3) + 1 / (3 × 4) + 1 / (4 × 5) + … 
= 1 + 1 – 1/2 + 1/2 – 1/3 + 1/3 – 1/4 + 1/4 – 1/5 + … 
= 2

別忘了， 1 + 1 / 2 2 + 1 / 3 2 + 1 / 4 2 + 1 / 5 2 + …是我們把所求的概率值取了倒數後的結果。因此，我們所求的概率值就應該大於1/2了。也就是說，這道題目的正確答案是A 。

可以證明， 1 + 1 / 2 2 + 1 / 3 2 + 1 / 4 2 + 1 / 5 2 + …實際上等於π 2 / 6 。因此，任意兩個正整數互質的概率就是6 / π 2 ≈ 0.608 。神奇的數學常數π經常會出現在一些與圓形八竿子打不著的地方，比如我們之前提過的Buffon投針問題。而大家剛才看到互質概率問題，才是我覺得最為經典的例子之一。

這篇文章中的題目是我長期收集而來的。大部分題目都是非常經典的題目，它們可以在The Colossal Book of Short Puzzles and Problems 、 Mathematical Puzzles: A Connoisseur's Collection 、 Mathematical Mind-Benders 、 Problems for Mathematicians, Young and Old 、 40 Puzzles and Problems in Probability and Mathematical Statistics 、 Fifty Challenging Problems in Probability 等書中找到。有些題目是我很早以前就寫過的，此處有所改寫。部分文字直接摘自《浴缸裡的驚嘆： 256 道讓你恍然大悟的趣題》。

直接摘自:http://www.matrix67.com/blog/archives/6665#more-6665