摘自:http://www.matrix67.com/blog/archives/5515
怎樣把一個鈍角三角形分成若干個銳角三角形
這是我最喜歡的幾何謎題之一:你能否在紙上畫一個鈍角三角形,然後把它分割成若干個銳角三角形?令人難以置信的是,這竟然是可以辦到的!繼續看下去之前,大家不妨先自己想一會兒。 

每次我在課堂上提出這個問題的時候,學生們總會瘋狂而盲目地進行嘗試。根據我的觀察,絕大多數人都會先畫一個不那麼鈍的鈍角三角形(其實這本質上並不會簡化我們的問題),然後作出一系列類似於圖1 的嘗試,但最後都以失敗告終。此時我往往會反復強調:要有方法啊,要有方法!首先,想必很多人已經註意到了,我們必須在鈍角里引出一條線(如圖2 所示),這樣才能把鈍角給消除掉。接下來,則是很少有人意識到的一點:我們不能讓這條線一直延伸到對邊,否則原三角形將會被分成一個銳角三角形和一個鈍角三角形(或者兩個直角三角形),這並不能解決根本問題。也就是說,這條線在到達對邊前就必須得分岔。最後一個關鍵的問題就是,分成幾岔?顯然,分成三岔(如圖3 所示)是不夠的,因為這樣只能把一個周角分成四份,它們不可能都是銳角。為了讓所有的角都是銳角,我們至少要讓這條線分成四岔(如圖4 所示)。最後,再把一些沒有連起來的點連起來,我們就得到一個像模像樣的答案了(如圖5 所示)。
有的讀者或許會說,等等,等等,你怎麼敢肯定,圖5 中的每個小三角形都是銳角三角形呢?其實,我也不敢肯定。不過,我並沒有說圖5 就是最終的答案。為了證明確實有一個鈍角三角形能被分成若干個銳角三角形,我們需要給出一個確鑿的、能供他人進行驗證的例子。圖5 並不是一個確鑿的例子,但它給我們提供了構造這種例子的思路,或者更貼切地說,構造這種例子的模板。借助這個模板,我們很容易得到下面這種構造方案。
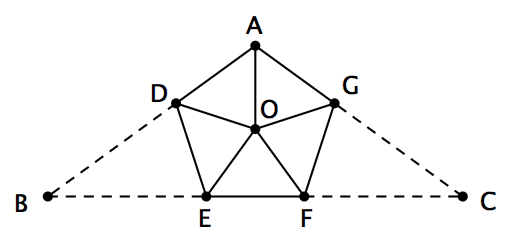
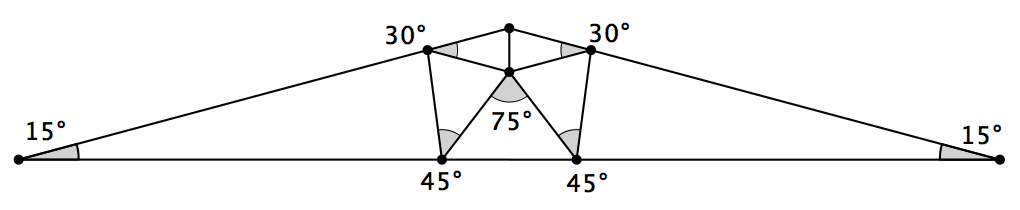
如圖,首先,畫一個正五邊形ADEFG 。然後,找出它的中心O ,將它分別與A 、 D 、 E 、 F 、 G 相連。最後,延長AD 和FE 並交於點B ,延長AG 和EF 並交於點C 。那麼,整個大三角形ABC 將會成為一個頂角為108° 的等腰三角形。這就是一個絕對讓人信服的例子,我們能精確地算出這裡面的每個小三角形的每個內角的度數,從而說明每個小三角形的確都是銳角三角形。
那麼,能否把任意一個鈍角三角形都分割成若干個銳角三角形呢?這下子,問題就變得複雜得多了。為了給出一個肯定的答案,我們必須想出一種能夠適用於所有鈍角三角形的通用分割方案,並且證明由此產生的小三角形確實都是銳角三角形。這個有名的問題最早出現在1960 年3 月的The American Mathematical Monthly 上,同年11 月,美國的一位中學數學老師Wallace Manheimer 給出了下面這個解答。
如圖,假設△ABC 中, ∠BAC 是鈍角。作出△ABC 的內心I 以及內切圓,將BI 、 CI 與圓的交點分別記作M 、 N 。過點M 作圓的切線,分別與AB 、 BC 交於D 、 E ;過點N 作圓的切線,分別與AC 、 BC 交於G 、 F 。最後,把D 、 E 、 F 、 G 都和內心I 相連,我們就把整個大三角形分成了7 個小三角形。
1961年,美國數學家Verner Hoggatt Jr.在The American Mathematical Monthly上發表了一篇論文,給出了一個更出人意料的結論:不但任意一個鈍角三角形都能被分割成若干個銳角三角形,而且任意一個鈍角三角形都能被分割成若干個等腰銳角三角形(即使這個鈍角三角形本身不是等腰的)!讓我們來看一看他是怎麼做到的。
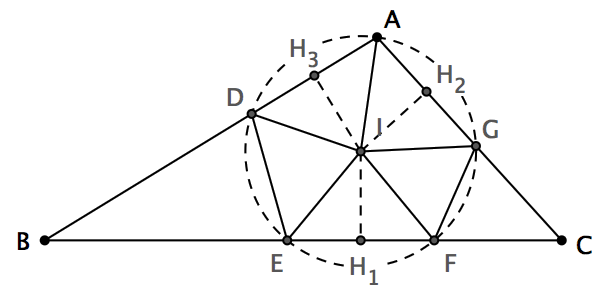
如圖,仍然假設△ABC中, ∠BAC是鈍角。還是作出△ABC的內心I ,還是以I為圓心,不過這一次,讓我們以IA為半徑作圓。這個圓一定會和△ABC交於另外四個點,不妨依次記作D 、 E 、 F 、 G (注意,這四個交點為什麼一定存在,這是需要嚴格說明的,不過這裡我們暫且略去) 。顯然, IA = ID = IE = IF = IG ,因而圓裡的五個小三角形都是等腰三角形。過I作三角形三邊的垂線段IH 1、 IH 2、 IH 3,由於內心I到三角形三邊的距離都相等,因此IH 1 = IH 2= IH 3。那麼, △IAD 、 △IAG 、 △IEF就成為了這麼一組等腰三角形,它們擁有相同的腰長,並且底邊上的高也都相等。由此可以推出,它們是一組全等三角形。另外,容易證明△BIH 1和△BIH 3全等,於是BH 1 = BH 3;同時, EH 1也是等於DH 3的,因而BE是等於BD的,可見△BDE是一個以B為頂點的等腰三角形。根據同樣的道理, △CFG也是一個以C為頂點的等腰三角形。由此可知,圖中的所有小三角形都是等腰三角形。
不過,為什麼每個小三角形都是銳角三角形呢?別忘了,等腰三角形的兩個底角一定都是銳角,因此,我們只需要說明每個小三角形的頂角也都是銳角就行了。∠B 和∠C 都是銳角,因而△BDE 和△CFG 都是銳角三角形了。不難算出, ∠AID 和∠AIG 都等於180° – ∠BAC ,因而△IAD 和△IAG 也都是銳角三角形了。△IEF 和它倆全等,自然也是一個銳角三角形。那麼, △IDE 和△IFG 呢?仔細算一算你會發現, ∠DIE = ∠BAC – ∠B , ∠FIG = ∠BAC – ∠C ,我們不能保證它們都是銳角。因此,最終我們只得到了一個暫時還不太完美的結果:如果三角形△ABC 中, ∠A 是鈍角,並且∠A – ∠B 和∠A – ∠C 都小於90°,那麼我們就可以把它分割成7 個等腰銳角三角形。
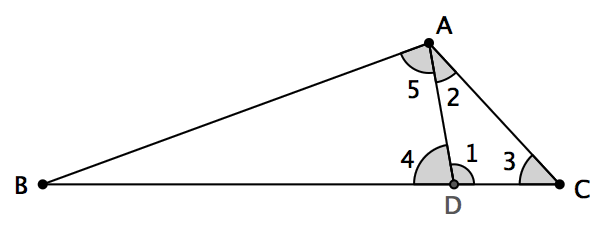
如果∠A – ∠B 和∠A – ∠C 當中至少有一個大於等於90° ,分割方案就會失效,這時又該怎麼辦呢?Verner Hoggatt Jr. 想到了極其聰明的一招。如圖,仍然假設∠BAC 是鈍角。剩下的兩個角∠B 和∠C 都是銳角。不妨假設其中∠B ≤ ∠C 。我們先在BC 上截取BD ,使得BD = BA (由於大角對大邊, BC > BA ,因此這是一定能辦到的)。△BAD 便成了一個以B 為頂點的等腰三角形。由於頂角∠B 是銳角,因而△BAD 是銳角三角形。有人或許會說,剛才不是說過,這樣不能解決根本問題嗎?△DAC 仍然是一個鈍角三角形呀?不過,這次就不一樣了: △DAC 將會滿足, ∠1 – ∠2 和∠1 – ∠3 都小於90° !這是因為:
∠1 – ∠2 = (180° – ∠4) – ∠2 = (180° – ∠5) – ∠2 = 180° – (∠5 + ∠2) = 180° – ∠BAC < 90°
並且由∠B ≤ ∠C 可知:
∠1 – ∠3 ≤ ∠1 – ∠B = (180° – ∠4) – ∠B = 180° – (∠4 + ∠B) = ∠5 < 90°
套用剛才的分割方案,我們就可以把△DAC 分成7 個等腰銳角三角形,從而把整個三角形△ABC 分成8 個等腰銳角三角形了。到此為止, Verner Hoggatt Jr. 就完整地證明了,任意一個鈍角三角形都可以被分成最多8 個等腰銳角三角形。

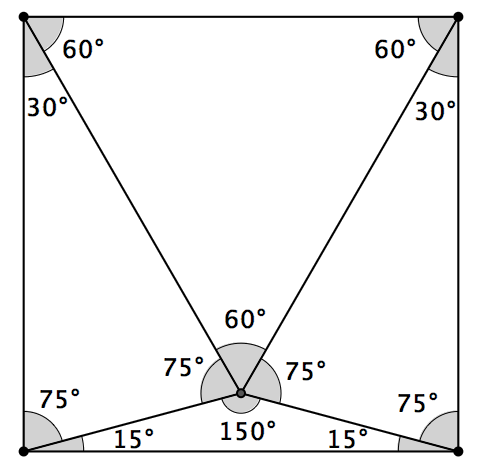
從最初的問題出發,我們還可以提出很多其他的擴展問題。比方說,一個正方形最少能被分成多少個銳角三角形?數學趣題大師Martin Gardner 曾經考慮過這個問題。他“想了好幾天,一度以為分成9 個是最少的,然後就突然想到了一種分成8 個的方法”,如上圖所示。他覺得8 個銳角三角形應該是最少的了,但卻不能證明這一點。隨後,數學圈子裡出現了好幾個嚴密程度不同的證明。值得一提的是,這個問題還曾經作為一道題目,出現在了1967 年的IMO 候選題裡。
同樣地,我們也可以問,一個正方形最少能被分成多少個等腰的銳角三角形?我們可以先像上圖那樣把正方形分成四個等腰三角形。其中三個等腰三角形已經是銳角三角形了,利用Verner Hoggatt Jr. 的方法則可以把最下面那個鈍角三角形分成8 個等腰銳角三角形,於是最終把正方形分成了11 個等腰銳角三角形。然而,注意到最下面那個鈍角三角形其實本來就是等腰的,這對於我們來說非常有利;或許把它分成等腰銳角三角形時,分成8 個並不是必需的。事實上,利用下圖所示的方法,我們可以把它分成7 個等腰銳角三角形,因而最終把正方形分成了10 個等腰銳角三角形。不過, 10 個究竟是不是最少的,這似乎還有待進一步探討。
類似地,對於任意矩形,或者任意凸四邊形,或者任意四邊形,或者任意n邊形來說,如何把它們分成盡可能少的銳角三角形,或者把它們分成盡可能少的等腰銳角三角形,這些問題都還有待繼續研究。在計算機圖形處理中,我們往往需要對圖形進行三角剖分;如果所有三角形都是銳角三角形的話,這會給我們帶來很多有用的性質。因此,直到現在,人們仍然有足夠的動機和熱情去研究圖形的銳角三角形剖分。關於最近幾年這方面的一些進展以及仍然有待解決的問題,可以參見Carol Zamfirescu的這篇論文:
看到這個除了驚艷外
跟同事分享
同事說這就是鴿攏的應用
我想到的是
我做出這七個三角形
請他拼出鈍角三角形
會困難嗎?
會唯一嗎?
越想越開心,
經過的學生問我
一大早再開心什麼?
看到這個除了驚艷外
跟同事分享
同事說這就是鴿攏的應用
我想到的是
我做出這七個三角形
請他拼出鈍角三角形
會困難嗎?
會唯一嗎?
越想越開心,
經過的學生問我
一大早再開心什麼?
沒有留言:
張貼留言