所有的問題 都是人 在現實 和期望值中的落差造成的

我們很常遇到一種情況
在甲可能覺得是很大的問題
可是乙會覺得這根本不是問題
所以有人說
「真正的問題不在問題本身，
    而是面對問題的態度」
 黃執中 曾經說過一個很有趣的觀點
「所有的問題都是
   人在期待和現實之間的落差造成」
所以問題不是客觀存在的
而是可以被人創造出來的

你如果問一個穩定交往中的女孩子：
你的男朋友有沒有問題
她可能會回答你：
很好啊！沒有問題。
 那如果我問：
那你的男朋友是你能想像中最好的男朋友嗎？
 這時她可能就會開始想：
或許 他可以再體貼一點
或許 可以再帥一點 再高一點…

 為什麼呢？
因為當我問妳：他是最好的嗎？
 我把你的期待瞬間提到非常高
這時和現實的差距讓你無法忽視

 所以是不是當我們說：
這個學生的態度有問題
其實背後真正的意思就是
你的態度和我的期待有落差
當學生說：
老師的管教有問題
其實背後的真正的意思是
老師的管教和我的期待有落差
讓我們說：
這個世代的孩子有問題
其實背後真正的意思是
這個世代的孩子的表現
和我們的期待 有落差

以前在我們那個年代
很多爸媽 對孩子的期待 就是
 不要變壞 可以 好好工作 養活自己
現在 這個世代
 大部分的爸媽都希望
 孩子可以「成材」

所以很多時候
當問題發生了  要確認一下
是現實中不夠努力
還是期待太高了
造成「太有感的差距」

你 一定會想問：
難道沒有期待就沒有問題了嗎？
當然不是
如果 都沒有期待那就是
你的期待出了問題
你的期待和現實中該有的期待產生了落差

而數學的思維訓練就是
讓你更加看清問題的本質
至於 問題本身有沒有解決
其實有時並不是最重要急迫的
因為有些問題本身就無解
或是現在是無解

怎麼說？
數學在所有學科中算是
最可以接受無解的情況了
因為我們知道
有時候無解是時空背景不夠成熟造成的

就像國中小會說
x^2+1=0   沒有（實數）解
可是高中生都知道
他有一種較特別的型式  虛根

有時候 不能解決
只是 因為  現在沒辦法解決

數學的思維 很多時候
不一定能幫你解決人生的問題
但是它一定可以協助你
在問題的思考中更清楚了解真正的問題
當你能夠看清問題中的問題
妳也比較能夠想清楚
你真的想要的是什麼
而人生很多時候
如果你可以想得夠清楚
那麼也就夠了

圓周上均勻分佈著100 個點。隨便選擇兩個點連一條線段，再隨便選擇另外兩個點連一條線段。那麼，下面哪種情況的可能性更大一些？

A．兩條線段相交
B．兩條線段不相交
C．上述兩種情況的出現概率相同

這個題目的答案是B 。隨便選擇兩個點，再隨便選擇另外兩個點，本質上相當於先隨便選擇四個點，再決定把這四個點配成怎樣的兩對。對於任意四個點A 、 B 、 C 、 D （在圓周上按此順序排列）來說，我們都有三種不同的配對方案：① A – B, C – D ② A – C, B – D ③ A – D, B – C 。其中，只有方案② 對應的兩條連線才會相交。因此，兩條線段相交的概率是1/3 。

不透明的盒子裡有1000 張紙條，上面分別寫有1, 2, 3, …, 1000。A 從盒子裡隨機取出100 張紙條，並把這100 張紙條上的數從小到大排成一排。然後， B 從盒子裡剩下的紙條中隨機取出1 張紙條，並看看這張紙條上的數在A 那裡排第幾位。例如，如果A 手中的數有50 個比B 取出的大，另外50 個比B 取出的小，那麼B 手中的數就排第51 位。那麼，下面哪種情況的可能性更大一些？

A．B手中的數排第1位
B．B手中的數排第51位
C．上述兩種情況的出現概率相同

很多人的直覺都是，排第1 可能性不大，排中間可能性更大。而實際上，考慮所有101 個數的101! 種排列方案，或者從1000 個數里選101 個數所產生的P(1000, 101) 種排列方案， B 選的那個數將會等可能地出現在各個位置。因此，這個題目的答案是C 。

如果你還想不明白的話，你乾脆直接想成是， A 抽了100 個數，然後再幫B 抽了一個數，問幫B 抽的這個數更有可能排第幾。如果你還想不明白的話，你乾脆直接想成是， A 抽了101 個數，問最後抽出的這個數更有可能排第幾。如果你還想不明白的話，你乾脆直接想成是， A 選了101 個數往空中一撒，問最後一個落地的數更有可能是排第幾的數。

把一副洗好的牌（共52 張）背面朝上地摞成一摞，然後依次翻開每一張牌，直到翻出第一張A 。那麼，下面哪種情況的可能性更大一些？

A．翻開第3張牌時出現了第一張A 
B．翻開第4張牌時出現了第一張A 
C．上述兩種情況的出現概率相同

這個題目的答案是A 。這個答案並不出人意料。你不妨考慮一個非常極端的情況：假設一副牌裡只有三張牌，其中兩張是A ，另外一張是2 。那麼，洗好牌後，三張牌的順序有AA2, A2A, 2AA三種（如果把兩張A看作是兩張不同的A ，那麼三張牌的順序有A 1 A 2 2, A 2 A 1 2, A 1 2A 2 , A 2 2A 1 , 2A 1 A 2 , 2A 2 A 1六種）。翻到第1, 2, 3張牌時出現第一張A的概率分別是2/3, 1/3, 0 。

至於原題為什麼選A ，我們給出一個這樣的解釋。洗好牌後，從前往後四張A 所在的位置一共有C(52, 4) 種可能的情況，分別為(1, 2, 3, 4), (1, 2, 3, 5), ( 1, 2, 3, 6), …, (49, 50, 51, 52) 。其中，形如(3, ?, ?, ?) 的情況顯然比形如(4, ?, ?, ?) 的情況更多，因為前者的問號處可以有更豐富的取值。

把一副洗好的牌（共52 張）背面朝上地摞成一摞，然後依次翻開每一張牌，直到翻出第一張A 。那麼，下面哪種情況的可能性更大一些？

A．再下一張牌是黑桃A 
B．再下一張牌是黑桃2 
C．上述兩種情況的出現概率相同

很多人可能會認為，下一張牌是黑桃2 的可能性更大，因為剛才翻出的首張A 可能就是黑桃A 。其實這種直覺是錯誤的。令人吃驚的是，這道題的答案是C 。下一張牌是黑桃A 的概率與下一張牌是黑桃2 的概率一樣大，它們都等於1/52 。

為了說明這一點，我們不妨來看一種同樣能實現絕對隨機的另類洗牌方式：先把一副牌中的黑桃A 抽出來，隨機洗牌打亂剩下51 張牌的順序，然後把黑桃A 插回這摞牌中（包括最頂端和最底端在內，共有52 個可以插入的位置）。顯然，黑桃A 正好插到了這摞牌的首張A 下面有1/52 的可能性。根據同樣的道理，首張A 下面是黑桃2 的概率也是1/52 。事實上，任何一張牌都有可能出現在首張A 的下面，它們出現的概率是相等的，都等於1/52 。

 摘自:http://www.matrix67.com/blog/archives/6665#more-6665

在一根木棒上隨機選擇兩個點，並在這兩個點處下刀，把木棒砍成三段。下面哪種情況的可能性更大一些？

A．這三段木棒能拼成一個三角形
B．這三段木棒不能拼成一個三角形
C．上述兩種情況的出現概率相同

這個題目選B 。我們可以證明，這三段木棒能拼成三角形的概率是1/4 。不妨把這根木棒的長度設為1 ，兩個分割點的位置分別記作x 、 y ，則x 和y 都是0 到1 之間的隨機數。那麼，所有可能的(x, y) 組合就對應了正方形(0, 1) × (0, 1) 內的所有點。三段木棒能拼成三角形，當且僅當(x, y) 落在了陰影部分。由於陰影部分佔了總面積的1/4 ，因此這三段木棒能拼成三角形的概率就是1/4 。

這個題目還有很多變種。比如，如果先把木棒隨機砍成兩段，再把較長的那段木棒隨機砍成兩段，問這三段木棒能拼成一個三角形的概率是多少。這該怎麼解呢？你或許會說，為何不像剛才那樣，把第一個分割點和第二個分割點的位置分別記作x 、 y ，然後套用剛才的面積大法？這次就不行了，因為y 的值不再能獨立而均勻地分佈在0 到1 之間。但是，我們可以令x 為第一個分割點在整根木棒上的比例，令y 為第二個分割點在較長的那段木棒上的比例。舉個例子， (x, y) = (1/3, 1/3) 的意思就是，先把整根木棒砍成1 : 2 兩段，再把較長的那段木棒砍成1 : 2兩段。這樣一來，所有可能的(x, y) 組合就再一次均勻地對應了正方形(0, 1) × (0, 1) 內的所有點。最終，三段木棒能拼成三角形，當且僅當(x, y) 落在由x · y < 1/2, (1 – x) · y < 1/2, x · (1 – y) < 1/2, (1 – x) · (1 – y) < 1/2 組成的交集區域裡。利用定積分可以求出，這部分區域的面積佔整個正方形面積的2 · ln(2) – 1 ≈ 38.63% 。這就是答案。

著名的Buffon 投針問題，標準解法之一也用到了這種模型。在地板上畫一系列間隔為1 厘米的平行直線，然後把一根1 厘米長的針扔到地板上，它與直線有交點的概率是多少？令x 為這根針的中心到離它最近的那條直線的距離，令y 為這根針與平行線的夾角。所有可能的針的位置，就可以用所有可能的(x, y) 組合來表示，它們正好對應了矩形(0, 1/2) × (0, π/2) 內的所有點。其中，合法的區域為y < arccos(2x) ，它佔矩形面積的2 / π ≈ 63.66% 。這就是答案。

高中數學課本把這種解決概率問題的模型叫做“幾何概型”。說到幾何概型，最經典的可能要算下面這個例題。A 、 B 兩人約定好晚上6:00 到7:00 之間在公園門口見面。每個人都會從6:00 到7:00 這段時間當中隨機挑選一個時間，並在這個時間到達公園門口。每個人都只願意等待15 分鐘，也就是說，如果15 分鐘之後沒有看見對方，那麼就立即離開。那麼，兩人最終能見面的概率有多大？答案是7/16 。

答案是有的，而且這個簡單的方法甚至不需要語言。
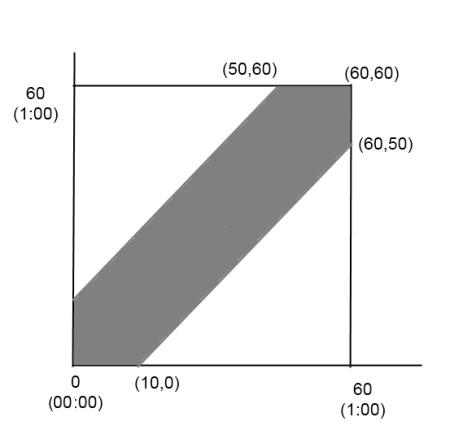從上圖中，你能一眼看出結果麼？
如果把甲的到達的時間記在x 軸上，把乙的到達時間記在y 軸上，那麼他們到達的時間便可以用坐標系中的點( x , y ) 來表示，根據設定可知這個點一定會落在圖中的正方形區域中。而如果二人想見面，那麼他們先後到達的時間間隔一定要小於十分鐘，即| x – y | ≤ 10。
解這個不等式，可得x – 10 ≤ y ≤ x + 10 。將這兩條支線在坐標系中畫出來，就能發現它們圍成的區域正好是上圖的陰影部分。
換言之，如果兩人要碰面，對應的到達的時間點（x，y） 就必須要落在陰影部分內。所以陰影部分的面積與大正方形面積之比就是所要求的概率，據此我們就能很輕鬆地計算出答案：11／36。

(摘自羅胖60秒)
話說有個朋友，有一天，他上小學的女兒問他，“趨勢”這個詞是什麼意思？他想半天也回答不上來。對啊，這麼熟悉的一個詞，真要讓你解釋，你還會覺得挺難說明白的。我再舉個例子，比如說“嘮叨”這個詞，每個人都理解吧？但它到底是什麼意思？是話多？不是，相聲演員也話多，就不是嘮叨。是說小事？不是，很多閒聊也是說小事，也不是嘮叨。是說煩人的話？很多冒犯人的話也不見得是嘮叨啊。還是吳伯凡老師有一次一語點醒夢中人。他說，“嘮叨”就是說沒有對象感的話，沒有選擇地看見什麼就說什麼。你看，從小就知道這個詞，也會用，對它有精準的語感，但是沒有高人點醒，我們還是不能準確地描述它。所以你看，學習，並不僅僅是指要學習陌生的東西，在熟悉的世界裡也有大量的盲區啊。

萬維鋼老師的《精英日課》第三季，昨天回歸了。他在發刊詞裡面講了一個有趣的知識點。如果一個商家承諾你，你在這兒買了東西，一個月之內，只要發現其他商家價格比我們低，那我們不但會補足差價，而且還會多給你差價的10%，做為補償。哎，這商家為什麼這麼做？是業界良心，還是其中有詐呢？其實都不是。你想，他這麼宣布了之後，就避免了價格戰。其他商家再降價也不能從他這兒搶走顧客，那其他商家為什麼還要降價呢？看似是自殘的做法，其實保證了價格的穩定，商家還是獲利的。你看，看問題，有兩種視角，個人視角和全局視角。個人視角你能得出評價，而全局視角才能看到真相。所以，萬維鋼老師把有全局視角的人稱之為“手眼通天”的人。他說，這才是他《精英日課》的服務對象

數學趣談

今天跟學生說 遞移律不可以亂用 a愛b B愛C 不代表A就愛C
面對 被動的 回答 我們可以再回答的時候想要提出附加條件式的問題的解決4分美滿無懈可擊 最有名的例子 就是 大家問東京的人找法律應該用什到大事 問耶穌該怎麼處理 耶穌如果不同意那就是違反法令如果同意那這樣神愛世人救世主的形象就會違背 耶穌的回答是 你們之中是沒有犯過錯的就可以拿石頭砸死他大家反躬自問都覺得自己並不乾淨就一個一個太厲害了

努力不能讓你的人生完美 卻可以讓你的人生完整

這幾天一個家齊的學生私訊我
說想跟我聊
聊了一下 才知道他想報名古都 半馬
卻又害怕 跑不完
 我跟他分析
其實門檻很低
一般男生快走一個小時可以到6公里
 3.5個小時 21公里
 只要不停下來
 基本上都可以達到 …

而且我問他
 跑不完會怎麼樣嗎？
很丟臉嗎？
我聽過你們班上的同學是這樣說的
我們不可能做到
別人太優秀了
我們就是一個魯蛇 …

逃避挫折很容易
比堅持 一直努力容易多了
一直不為想要的事情用力
一直不做挑戰自我的事情
當然永遠都不會挫折
因為他根本沒有「資格」遭遇挫折

 你不一樣
 當你出發了
 你的人生就多了一段的體驗
 人生有幾回 可以 讓你
用盡全力 放盡力氣
你有多久 沒有用盡全力去做一件事情
你有多久 沒有拼搏到感動自己
順利完成很好
就算最後有些遺憾
也比 總是想像
體驗了更多的風景
我當下沒跟你說
其實做這些事
 或許不會讓你的人生更「完美 」
但我相信會讓你的人生 更「完整」
就像鳥類飛過天際
對天空而言
 不會留下什麼
不會改變什麼
可是 對鳥自己而言
他知道
有些改變發生了
 因為 他看過了
更精彩的人生風景
…

我常鼓勵學生
至少去參加一次半馬和全馬
甚至變成一個 成年禮的儀式
 如果可以
在過程中 告訴自己 要邁入下一個階段
就算跑到沒有體力 更好
那反而更容易進入自我的對話
會問自己
 我到底為什麼要這樣虐待自己
我到底真的想要的是什麼
我之前到底在過什麼樣的生活…


有趣的是
我跟黃小妹提到這件事
玉妹馬上回答 說
這有什麼好考慮的就報名啊
我說可是他怕跑不完啊
 玉妹說
我都可以環島回來了
跟你學生說有什麼好怕的
做就對了…

 看著黃玉妹
我發現 暑假這趟旅程
她 真的有改變了

我笑著跟黃玉妹說
妹妹你是不是覺得環島回來
在家裡的地位提升了
快可以跟我平起平坐了
她說
想太多
你一直是最低的
 我只是拉大我們的差距而已…

掛畫問題

2011年度最变态的迷宫难题

    下面大家将会看到的是一个极其简单而又极其复杂的“迷宫”，这无疑是我在本年度见到的最变态的谜题：从左边入口处的 2011 进去，在迷宫里转悠，最后变成 2012 从右边出来。你可以在迷宫里转圈，可以重复之前走过的路，但不能往回退着走。

      

    你能成功走出来吗？

    放弃吧，答案是

2011 +7 ÷2 +7 ÷2 +7 -5 ×3 ÷2 +7 ÷2 +7 ×3 -5 ÷2 +7 ÷2 +7 -5 ×3 -5 ×3 ÷2 +7 -5 ×3 ÷2 +7 -5 = 2012

    这个变态的谜题来自 Holiday Puzzles 2011 ，作者是 Erich Friedman 。
    提前祝大家新年快乐。

12個經典的行程問題

    無論是小學奧數，還是公務員考試，還是公司的筆試面試題，似乎都少不了行程問題——題目門檻低，人人都能看懂；但思路奇巧，的確會難住不少人。平時看書上網與人聊天和最近與小學奧數打交道的過程中，我收集到很多簡單有趣而又頗具啟發性的行程問題，在這裡整理成一篇文章，和大家一同分享。這些題目都已經非常經典了，絕大多數可能大家都見過；希望這裡能有至少一個你沒見過的題目，也歡迎大家來信提供更多類似的問題。

    讓我們先從一些最經典最經典的問題說起吧。選中空白部分顯示答案。

    甲、乙兩人分別從相距100 米的A 、B 兩地出發，相向而行，其中甲的速度是2 米每秒，乙的速度是3 米每秒。一隻狗從A 地出發，先以6 米每秒的速度奔向乙，碰到乙後再掉頭沖向甲，碰到甲之後再跑向乙，如此反复，直到甲、乙兩人相遇。問在此過程中狗一共跑了多少米？

    這可以說是最經典的行程問題了。不用分析小狗具體跑過哪些路程，只需要注意到甲、乙兩人從出發到相遇需要20秒，在這20秒的時間裡小狗一直在跑，因此它跑過的路程就是120米。
    說到這個經典問題，故事可就多了。下面引用某個經典的數學家八卦帖子： John von Neumann曾被問起一個中國小學生都很熟的問題：兩個人相向而行，中間一隻狗跑來跑去，問兩個人相遇後狗走了多少路。訣竅無非是先求出相遇的時間再乘以狗的速度。Neumann當然瞬間給出了答案。提問的人失望地說你以前一定聽說過這個訣竅吧。Neumann驚訝道：“什麼訣竅？我就是把狗每次跑的都算出來，然後計算無窮級數⋯⋯”

    某人上午八點從山腳出發，沿山路步行上山，晚上八點到達山頂。不過，他並不是勻速前進的，有時慢，有時快，有時甚至會停下來。第二天，他早晨八點從山頂出發，沿著原路下山，途中也是有時快有時慢，最終在晚上八點到達山腳。試著說明：此人一定在這兩天的某個相同的時刻經過了山路上的同一個點。

    這個題目也是經典中的經典了。把這個人兩天的行程重疊到一天去，換句話說想像有一個人從山腳走到了山頂，同一天還有另一個人從山頂走到了山腳。這兩個人一定會在途中的某個地點相遇。這就說明了，這個人在兩天的同一時刻都經過了這裡。

      

    甲從A 地前往B 地，乙從B 地前往A 地，兩人同時出發，各自勻速地前進，每個人到達目的地後都立即以原速度返回。兩人首次在距離A 地700 米處相遇，後來又在距離B 地400 米處相遇。求A 、 B 兩地間的距離。

    答案： 1700 米。第一次相遇時，甲、乙共同走完一個AB 的距離；第二次相遇時，甲、乙共同走完三個AB 的距離。可見，從第一次相遇到第二次相遇的過程花了兩個從出發到第一次相遇這麼多的時間。既然第一次相遇時甲走了700 米，說明後來甲又走了1400 米，因此甲一共走了2100 米。從中減去400 米，正好就是A 、 B 之間的距離了。

    甲、乙、丙三人百米賽跑，每次都是甲勝乙10 米，乙勝丙10 米。則甲勝丙多少米？

    答案是19 米。“乙勝丙10 米”的意思就是，等乙到了終點處時，丙只到了90 米處。“甲勝乙10 米”的意思就是，甲到了終點處時，乙只到了90 米處，而此時丙應該還在81 米處。所以甲勝了丙19 米。

    哥哥弟弟百米賽跑，哥哥贏了弟弟1 米。第二次，哥哥在起跑線處退後1 米與弟弟比賽，那麼誰會獲勝？

    答案是，哥哥還是獲勝了。哥哥跑100 米需要的時間等於弟弟跑99 米需要的時間。第二次，哥哥在-1 米處起跑，弟弟在0 米處起跑，兩人將在第99 米處追平。在剩下的1 米里，哥哥超過了弟弟並獲得勝利。

    如果你上山的速度是2 米每秒，下山的速度是6 米每秒（假設上山和下山走的是同一條山路）。那麼，你全程的平均速度是多少？

    這是小學行程問題中最容易錯的題之一，是小孩子們死活也搞不明白的問題。答案不是4米每秒，而是3米每秒。不妨假設全程是S米，那麼上山的時間就是S/2 ，下山的時間就是S/6 ，往返的總路程為2S ，往返的總時間為S/2 + S/6 ，因而全程的平均速度為2S / (S/2 + S/6) = 3 。
    其實，我們很容易看出，如果前一半路程的速度為a ，後一半路程的速度為b ，那麼總的平均速度應該小於(a + b) / 2 。這是因為，你會把更多的時間花在速度慢的那一半路程上，從而把平均速度拖慢了。事實上，總的平均速度應該是a和b的調和平均數，即2 / (1/a + 1/b) ，很容易證明調和平均數總是小於等於算術平均數的。

    接下來的兩個問題與流水行船有關。假設順水時實際船速等於靜水中的船速加上水流速度，逆水時實際船速等於靜水中的船速減去水流速度。

    船在靜水中往返A 、 B 兩地和在流水中往返A 、 B 兩地相比，哪種情況下更快？

    這是一個經典問題了。答案是，船在靜水中更快一些。注意船在順水中的實際速度與在逆水中的實際速度的平均值就是它的靜水速度，但由前一個問題的結論，實際的總平均速度會小於這個平均值。因此，船在流水中往返需要的總時間更久。
    考慮一種極端情況可以讓問題的答案變得異常顯然，頗有一種荒謬的喜劇效果。假設船剛開始在上游。如果水速等於船速的話，它將以原速度的兩倍飛速到達折返點。但它永遠也回不來了⋯⋯

    船在流水中逆水前進，途中一個救生圈不小心掉入水中，一小時後船員才發現並調頭追趕。則追上救生圈所需的時間會大於一個小時，還是小於一個小時，還是等於一個小時？

    這也是一個經典問題了。中學物理競賽中曾出現過此題，《編程之美》上也有一個完全相同的問題。答案是等於一個小時。原因很簡單：反正船和救生圈都被加上了一個水流的速度，我們就可以直接拋開流水的影響不看了。換句話說，我們若以流水為參照系，一切就都如同沒有流水了。我們直接可以想像船在靜水噹中丟掉了一個救生圈並繼續前行一個小時，回去撿救生圈當然也還需要一個小時。
    每當有人還是沒想通時，我很願意舉這麼一個例子。假如有一列勻速疾馳的火車，你在火車車廂裡，從車頭往車尾方向步行。途中你掉了一個錢包，但繼續往前走了一分鐘後才發現。顯然，你回去撿錢包需要的時間也是一分鐘。但是，錢包不是正被火車載著自動地往遠方走嗎？其實，既然你們都在火車上，自然就可以無視火車的速度了。前面的救生圈問題也是一樣的道理。

    下面這個問題也很類似：假設人在傳送帶上的實際行走速度等於人在平地上的行走速度加上一個傳送帶的速度。

    你需要從機場的一號航站樓走到二號航站樓。路途分為兩段，一段是平地，一段是自動傳送帶。假設你的步行速度是一定的，因而在傳送帶上步行的實際速度就是你在平地上的速度加上傳送帶的速度。如果在整個過程中，你必須花兩秒鐘的時間停下來做一件事情（比如蹲下來系鞋帶），那麼為了更快到達目的地，你應該把這兩秒鐘的時間花在哪裡更好？

    這個漂亮的問題出自Terence Tao 的Blog （http://terrytao.wordpress.com/2008/12/09/an-airport-inspired-puzzle）。很多人可能會認為，兩種方案是一樣的吧？然而，真正的答案卻是，把這兩秒花在傳送帶上會更快一些。這是因為，傳送帶能給你提供一些額外的速度，因而你會希望在傳送帶上停留更久的時間，更充分地利用傳送帶的好處。因此，如果你必須停下來一會兒的話，你應該在傳送帶上多停一會兒。

    假設你站在甲、乙兩地之間的某個位置，想乘坐出租車到乙地去。你看見一輛空車遠遠地從甲地駛來，而此時整條路上並沒有別人與你爭搶空車。我們假定車的行駛速度和人的步行速度都是固定不變的，並且車速大於人速。為了更快地到達目的地，你應該迎著車走過去，還是順著車的方嚮往前走一點？

    这是我在打车时想到的一个问题。我喜欢在各种人多的场合下提出这个问题，此时大家的观点往往会立即分为鲜明的两派，并且各有各的道理。有人说，由于车速大于人速，我应该尽可能早地上车，充分利用汽车的速度优势，因此应该迎着空车走上去，提前与车相遇嘛。另一派人则说，为了尽早到达目的地，我应该充分利用时间，马不停蹄地赶往目的地。因此，我应该自己先朝目的地走一段路，再让出租车载我走完剩下的路程。
    其实答案出人意料的简单，两种方案花费的时间显然是一样的。只要站在出租车的角度上想一想，问题就变得很显然了：不管人在哪儿上车，出租车反正都要驶完甲地到乙地的全部路程，因此你到达乙地的时间总等于出租车驶完全程的时间，加上途中接人上车可能耽误的时间。从省事儿的角度来讲，站在原地不动是最好的方案！
    我曾经把这个有趣的问题搬上了《新知客》杂志 2010 年第 9 期的趣题专栏（http://www.matrix67.com/blog/archives/3677）。不少人都找到了这个题的一个 bug ：在某些极端情况下，顺着车的方向往前走可能会更好一些，因为你或许会直接走到终点，而此时出租车根本还没追上你！

    某工厂每天早晨都派小车按时接总工程师上班。有一天，总工程师为了早些到工厂，比平日提前一小时出发步行去工厂。走了一段时间后，遇到来接他的小车才上车继续前进。进入工厂大门后，他发现只比平时早到 10 分钟。总工程师在路上步行了多长时间才遇到来接他的汽车？设人和汽车都做匀速直线运动。

    据说，这是一道初中物理竞赛题（初中物理有“运动”一章）。答案是 55 分钟。首先，让我们站在车的角度去想（正如前一题那样）。车从工厂出发，到半途中就遇上了总工程师并掉头往回走，结果只比原来早到 10 分钟。这说明，它比原来少走了 10 分钟的车程，这也就是从相遇点到总工程师家再到相遇点的路程。这就说明，从相遇点到总工程师家需要 5 分钟车程。
    现在，让我们把视角重新放回总工程师那里。让我们假设总工程师遇上了来接他的车并坐上去之后，并没有下令汽车立即掉头，而是让车像平日那样继续开到他家再返回工厂，那么他到工厂的时间应该和原来一样。这说明，他提前出发的那一个小时完全浪费了。这一个小时浪费在哪儿了呢？浪费在了他步行到相遇点的过程，以及乘车又回到家的过程。既然乘车又回到家需要 5 分钟，因此步行的时间就是 55 分钟了。

    有一位隐居在深山老林的哲学家。一天，他忘记给家里唯一的时钟上发条了。由于他家里没有电话、电视、网络、收音机等任何能获知时间的设备，因此他彻底不知道现在的时间是多少了。于是，他徒步来到了他朋友家里坐了一会儿，然后又徒步回到自己家中。此时，他便知道了应该怎样重新设定自己的时钟。他是怎么做的？
    很多人的第一想法或许是观察日出日落。在此，我们也假设通过太阳位置判断时间是不可靠的。 Update: 不少网友找到了此题的一个 bug 。在此我们假设，时钟是固定在墙上的，或者由于太重，无法直接带走。

    传统意义上说，这个问题不算行程问题。不过，在写这篇文章时，这个问题立即跳入我的脑海，我也就把它放进来了。
    答案：别忘了，他家里的时钟并不是不走了，只是不准了而已。因此，他可以借助自己家里的时钟，判断他此次出行一共花了多久。假设往返所花时间一样，再结合在朋友那儿看到的正确时间，他便能算出应该怎样调整自己的时钟了。

还有几个不太相关的经典问题这里没有提到，不过你或许会感兴趣：
汽车穿越沙漠问题：http://en.wikipedia.org/wiki/Jeep_problem
木杆上的蚂蚁：http://www.matrix67.com/blog/archives/3791 计算题1

贴着另一枚硬币旋转一周则自身转了两周：不同的解释方法

    有一道非常经典的智力问题：假设有两个一模一样的硬币 A 和硬币 B ，如果让硬币 B 不动，让硬币 A 贴着硬币 B 旋转一周，那么硬币 A 自身旋转了多少周？一个常见的错误答案是“显然也是一周啊”，而实际上正确的答案是两周，如下图所示。我们有很多方法来解释这种现象，其中最传统的说法便是“公转了一周，自转了一周”。硬币 A 的运动是由两部分合成的，公转一周（想像一个人绕着地球走了一圈），以及自转一周（想像一个轮子在地面上滚动了一周）。想像你是站在硬币 B 中心处的一个小人儿，看着硬币 A 贴着你脚下的硬币转动一圈。如果在此过程中，你始终面向硬币 A ，那么在你看来，硬币 A 似乎就是在长为 2πr 的平地上滚了一圈。而实际上，在观察硬币 A 的过程中，你自己也原地转了 360 度，因此从外面的人看来，硬币实际上转了两周。

      

    写了这篇文章后，我习惯性地开始用正多边形逼近的思路去分析一些与圆有关的一般性结论。在准备一份初中几何问题的材料时，我突然想到了上述问题的一个简单而漂亮的解释方法。

      

    考虑一个正方形贴着另一个正方形旋转一周，你会发现，前者自身也旋转了两周。容易验证，对于正三角形和正六边形，情况也都是如此。这一定不是巧合，或许对于所有的正 n 边形，结论都同样成立。仔细一想，你发现这很容易理解：对于正 n 边形来说，每转过一个顶点，转过的角度都相当于正 n 边形两个外角的大小。转过 n 个顶点回到出发位置后，正 n 边形显然转过了两倍的外角和，也就是 720 度。因而，正 n 边形自身旋转了两周。当正多边形的边数趋于无穷多时可知，一枚硬币贴着另一枚硬币旋转一周，则这枚硬币自身也一定正好旋转了两周。

不用三角函数求出∠BAC的度数

http://www.matrix67.com/blog/archives/5398#more-5398

趣题：不用三角函数求出∠BAC的度数

    今天看到了一道很有趣的几何题。如图，四边形 ABCD 中，连接对角线 AC 、 BD ，若 ∠ABD = 40° ， ∠ADB = 80° ， ∠CBD = 70° ， ∠CDB = 50° ，求 ∠BAC 的度数。

      

    这道题看上去似乎非常简单，但稍作尝试你就会发现，仅仅是在这几个角度之间来回倒腾，是没法求出 ∠BAC 的度数的。听说过 Langley 问题（就是那个臭名昭著的 20-80-80 三角形）的人就会知道，这种类型的题目往往会非常非常地复杂。据说这是 1989 – 1990 年加拿大亚伯达省中学数学竞赛中的一道题目，当时只有一个人做对，并且解答过程用到了非常繁琐的三角函数运算。然而，这道题实际上有一个非常漂亮的秒杀方法，完全不需要使用三角函数。你能想到吗？

      

    答案：把注意力集中在三角形 ABD 上。容易看出， ∠A = 180° – 40° – 80° = 60° 。另外， CB 平分 ∠B 的外角， CD 平分 ∠D 的外角，因而 C 就是三角形 ABD 的一个旁心。这说明， CA 也将平分 ∠A 。因此， ∠BAC = 60° / 2 = 30° 。

参考资料： Andy Liu, “A Better Angle From Outside”, Mathematical Horizons, November 1997

Marden定理

http://www.matrix67.com/blog/archives/5480#more-5480

數學之美：Marden定理

    如果叫我說出一個我最喜歡的數學定理，之前我可能會說Monge 定理；不過現在，我可能會說Marden 定理了：

         

設p(z)是一個複數域上的三次多項式， z 1、 z 2、 z 3是p(z)的三個根，它們在復平面上不共線。那麼，在這個複平面上存在唯一的橢圓，使得它與三角形z 1 z 2 z 3的各邊都相切，並且都切於各邊的中點處。並且，這個橢圓的兩個焦點是p'(z)的兩根。

    讀完這個結論以後，你一定會被數學之美深深地打動。這個結論出現在了Morris Marden於1945年發表的一篇論文裡，因而被Dan Kalman稱為Marden定理。Marden本人則認為，這個結論最早是由Jörg Siebeck在1864年發現並證明的。下面我們簡單地來證明一下這個結論，證明過程出自Dan Kalman在2008年發表的獲獎論文An Elementary Proof of Marden's Theorem。

    其實，結論的前半部分並不奇怪，對於任意一個三角形，內切於各邊中點的橢圓本來就是唯一的。這是很容易證明的，其中一種證明方法是，通過線性變換把這個三角形變形成一個等邊三角形，那麼內切於各邊中點的橢圓現在仍然是內切於各邊中點的橢圓，然而在一個等邊三角形中，內切於各邊中點的橢圓只有一個，就是這個等邊三角形的內切圓。關於這一點，詳細的證明可以參見這裡。

    因此， Marden 定理的核心就是：為什麼這個橢圓的兩個焦點就是p'(z) 的兩根。

    首先，讓我們來說明，為了證明Marden定理，我們可以把三角形z 1 z 2 z 3放置在復平面上的任意一個對我們有利的位置。因為，如果對於復平面上的某一個三角形來說命題是成立的，那麼任意地對這個三角形進行縮放、旋轉、平移，命題仍然是成立的。為什麼？這是因為，對三角形的縮放、旋轉、平移，說白了就是對三角形中的各個點進行變換操作M(z) = αz + β ，其中α和β是兩個固定的複數常數，並且α ≠ 0 。讓z與α相乘的結果就是對z進行縮放和旋轉，而β則表示在此之後平移量的大小。假設我們的命題對三角形z 1 z 2 z 3成立，對整個複平面進行上述變換後，三角形的三個頂點就分別移到了M(z 1 ) 、 M(z 2 ) 、 M(z 3 ) 。同時，三角形的內切橢圓以及橢圓的兩個焦點也都被順帶著移動了過去，內切橢圓還是內切橢圓，橢圓的焦點也還是橢圓的焦點。另外，原來的多項式是p(x) = (z – z 1 )(z – z 2 )(z – z 3 ) ，變換之後，新的多項式p M (x)就變成了(z – M( z 1 ))(z – M(z2 ))(z – M(z 3 )) 。假設原橢圓的兩個焦點分別是f 1和f 2，我們已經知道了它們正好是p'(z)的兩根。我們想要確認的就是，新橢圓的兩個焦點M(f 1)和M(f 2 )正好就是p M '(z)的兩個根。

    把p M (z)中的z全部用M(z)代換，得到：

         p M (M(z)) = (M(z) – M(z 1 ))(M(z) – M(z 2 ))(M(z) – M(z 3 ))

    注意到M(z) – M(z 1 )就等於α(z – z 1 ) （因為β被抵消了），同理，上式的後面兩個因式也分別等於α(z – z 2 )和α(z – z 3 ) 。於是，整個上式化簡為：

         p M (M(z)) = α 3 (z – z 1 )(z – z 2 )(z – z 3 )

    即：

         p M (M(z)) = α 3 · p(z)

    現在，在等式兩邊同時取導數（注意到M'(z) = α ），於是得到：

         α · p M '(M(z)) = α 3 · p'(z)

    也就是：

         p M '(M(z)) = α 2 · p'(z)

    這說明，如果f 1是p'(z)的根，那麼M(f 1 )也將是p M '(z)的根；類似地，如果f 2是p'(z)的根，那麼M (f 2 )也將是p M '(z)的根。這正是我們剛才想要說明的事情。

         

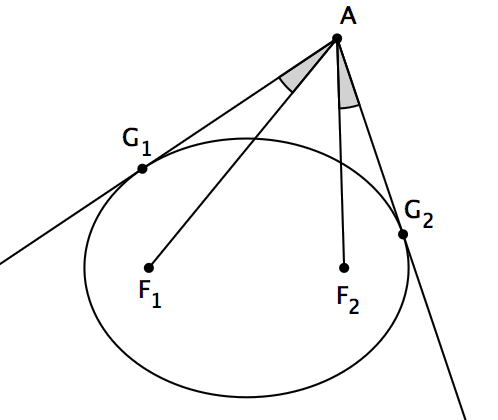
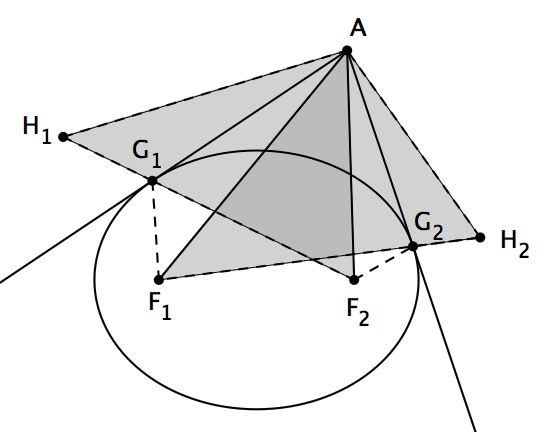
    為了證明Marden定理，我們還有一個準備工作要做。讓我們來證明下面這個引理：如圖， F 1、 F 2是給定橢圓的兩個焦點，過橢圓外的一點A向橢圓作兩條切線，切點分別為G 1和G 2，則有∠F 1 AG 1 = ∠F 2 AG 2。其實，這個引理包含了兩種不同的情況，如果把上面的G 1和G 2兩個點反過來標，我們將會得到另外一種情況。不過，如果我們證明了在第一種情況下結論始終成立，第二種情況也就自動地獲證了。因此，我們可以直接假設G 1和G 2的標法就如上圖所示。

         

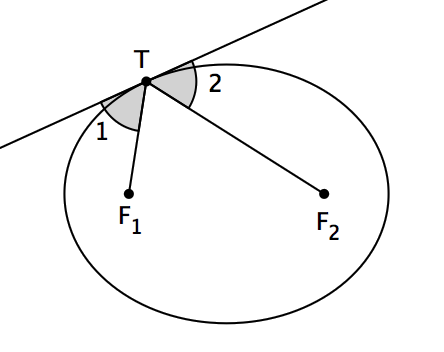
    證明這個引理需要用到與橢圓有關的一個非常經典的結論：從其中一個焦點出發的光線，射向橢圓內壁的任意一個位置，反射光線總會經過這個橢圓的另外一個焦點。換句話說，在上圖當中，過橢圓上的點T作切線，則∠1將會等於∠2 。你可以在這裡看到與橢圓的這個性質有關的更多討論。

         

    現在，沿著切線AG 1將F 1翻折到H 1，那麼H 1、 G 1、 F 2將會共線。類似地，沿著切線AG 2將F 2翻折到H 2，那麼H 2、 G 2、 F 1也將會共線。為了證明∠F 1 AG 1 = ∠F 2 AG 2，我們只需要證明∠F 1 AH 1 = ∠F 2 AH 2即可。

    由於H 1 F 2 = H 1 G 1 + G 1 F 2 = F 1 G 1 + G 1 F 2 = F 1 G 2 + G 2 F 2 = F 1 G 2 + G 2 H 2 = F 1 H 2，另外由剛才的翻折可知F 1 A = H 1 A ，並且F 2 A = H 2 A ，於是三角形AH 1 F 2和三角形AF 1 H2全等。這告訴我們∠H 1 AF 2 = ∠F 1 AH 2，同時減去一個公共部分後即得∠F 1 AH 1 = ∠F 2 AH 2，引理也就證到了。

    現在，我們已經準備好證明Marden定理了。我們首先說明，以p'(z)的兩根為焦點的橢圓，如果經過三角形z 1 z 2 z 3某條邊上的中點，則它一定會與這條邊相切。為此，我們把三角形的三個頂點擺放到復平面上的-1 、 1和w = a + bi三個位置，其中b > 0 ，於是p(z) = (z – 1)(z + 1)(z – w) = z 3 – w · z 2 – z + w 。對p(z)求導後得p'(z) = 3 · z 2 – 2 · w · z – 1 。

         

    假設p'(z)的兩根是f 1和f 2，則兩根之和f 1 + f 2 = 2 · w / 3 ，兩根之積f 1 · f 2 = – 1 / 3 。前一個式子說明了f 1和f 2當中至少有一個在x軸上方，而在後一個式子中， f 1 · f 2居然沒有虛數部分，這就說明了f 1和f 2其實都在x軸上方，並且θ 1 + θ 2 = 180° 。因而，如果以f 1和f 2為焦點，作一個過原點0的橢圓，則x軸就是一條經過該點的直線，它滿足∠1 = ∠2 ，這表明x軸就是橢圓在該點處的切線。而x軸其實就是三角形的底邊，原點0正是三角形底邊的中點！

    由於以同一對點為焦點只能作出一個與給定直線相切的橢圓，因而這就順便說明了，以p'(z)的兩根為焦點的橢圓，如果與三角形z 1 z 2 z 3的某條邊相切，則它一定會與這條邊切於中點處。

    最後我們來說明，以p'(z)的兩根為焦點的橢圓，如果與三角形z 1 z 2 z 3的其中一條邊相切了，則它一定會與三角形的三條邊都相切。由剛才的推論可知，所有的切點都將會是中點， Marden定理就證到了。這一次，讓我們把三角形的三個頂點放在0 、 1 、 w = a + bi三個位置，其中b > 0 。稍後我們將會看到，以p'(z)的兩根為焦點並且切於底邊的橢圓也會與0w相切。由對稱性，它一定也會和第三條邊相切。

    取p(z) = z(z – 1)(z – w) = z 3 – (1 + w) · z 2 + w · z 。求導得： p'(z) = 3 · z 2 – 2 · (1 + w) · z + w 。

         

    假設p'(z)的兩根是f 1和f 2。剛才我們已經知道了， f 1和f 2一定都在x軸的上方。不過這一次，兩根之積f 1 · f 2等於w / 3 。這告訴了我們什麼？這告訴了我們， θ 1 + θ 2 = θ ，換句話說， ∠1 = ∠2 ！假設以f 1和f 2為焦點作了一個橢圓， x軸正好是一條切線，那麼根據前面我們證過的那個結論，經過原點的另一條切線將會滿足∠1 = ∠2 ，這說明它與0w這條線重合。因而， 0w就是這另外一條切線。這就完成了Marden定理的最後一環。